
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的图象经过M(1,0)和N(3,0)两点,且与y轴交于D(0,3),直线l是抛物线的对称轴.
(1)求该抛物线的解析式.
(2)若过点A(﹣1,0)的直线AB与抛物线的对称轴和x轴围成的三角形面积为6,求此直线的解析式.
(3)点P在抛物线的对称轴上,⊙P与直线AB和x轴都相切,求点P的坐标.
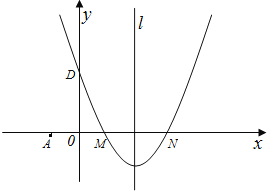
【答案】解:(1)∵抛物线y=ax2+bx+c(a≠0)的图象经过M(1,0)和N(3,0)两点,且与y轴交于D(0,3),
∴假设二次函数解析式为:y=a(x﹣1)(x﹣3),
将D(0,3),代入y=a(x﹣1)(x﹣3),得:
3=3a,
∴a=1,
∴抛物线的解析式为:y=(x﹣1)(x﹣3)=x2﹣4x+3;
(2)∵过点A(﹣1,0)的直线AB与抛物线的对称轴和x轴围成的三角形面积为6,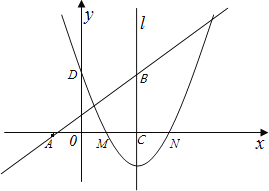
∴![]() AC×BC=6,
AC×BC=6,
∵抛物线y=ax2+bx+c(a≠0)的图象经过M(1,0)和N(3,0)两点,
∴二次函数对称轴为x=2,
∴AC=3,
∴BC=4,
∴B点坐标为:(2,4),
一次函数解析式为;y=kx+b,
∴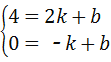 ,
,
解得:![]() ,
,
y=![]() x+
x+![]() ;
;
(3)∵当点P在抛物线的对称轴上,⊙P与直线AB和x轴都相切,
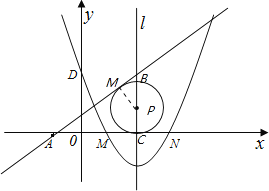
∴MO⊥AB,AM=AC,PM=PC,
∵AC=1+2=3,BC=4,
∴AB=5,AM=3,
∴BM=2,
∵∠MBP=∠ABC,
∠BMP=∠ACB,
∴△ABC∽△CBM,
∴![]() ,
,
∴![]() ,
,
∴PC=1.5,
P点坐标为:(2,1.5).
【解析】略


科目:初中数学 来源: 题型:
【题目】我们已经知道,形如![]() 的无理数的化简要借助平方差公式:
的无理数的化简要借助平方差公式:
例如: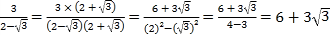 。
。
下面我们来看看完全平方公式在无理数化简中的作用。
问题提出:![]() 该如何化简?
该如何化简?
建立模型:形如![]() 的化简,只要我们找到两个数
的化简,只要我们找到两个数![]() ,使
,使![]() ,这样
,这样![]() ,
,![]() ,那么便有:
,那么便有:![]() ,
,
问题解决:化简![]() ,
,
解:首先把![]() 化为
化为![]() ,这里
,这里![]() ,
,![]() ,由于4+3=7,
,由于4+3=7,![]() ,
,
即(![]() ,
,![]() ,
,
∴![]()
模型应用1:
利用上述解决问题的方法化简下列各式:
(1)![]() ;(2)
;(2)![]() ;
;
模型应用2:
(3)在![]() 中,
中,![]() ,
,![]() ,
,![]() ,那么
,那么![]() 边的长为多少?(结果化成最简)。
边的长为多少?(结果化成最简)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,动点E、F分别从D、C两点同时出发,以相同的速度分别在边DC、CB上移动,当点E运动到点C时都停止运动,DF与AE相交于点P,若AD=8,则点P运动的路径长为( )

A. 8![]() B. 4
B. 4![]() C. 4π D. 2π
C. 4π D. 2π
查看答案和解析>>
科目:初中数学 来源: 题型:
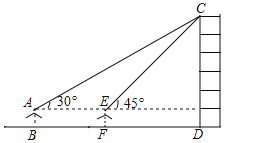
【题目】(7分)小敏同学测量一建筑物CD的高度,她站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走30m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据:![]() ,
,![]() .结果保留整数)
.结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①, 已知△ABC中, ∠BAC=90°, AB=AC, AE是过A的一条直线, 且B、C在AE的异侧, BD⊥AE于D, CE⊥AE于E.

(1)求证: BD=DE+CE.
(2)若直线AE绕A点旋转到图②位置时(BD<CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请给予证明;
(3)若直线AE绕A点旋转到图③位置时(BD>CE), 其余条件不变, 问BD与DE、CE的数量关系如何? 请直接写出结果, 不需证明.
(4)根据以上的讨论,请用简洁的语言表达BD与DE,CE的数量关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小月和小东在一起探究有关“多边形内角和”的问题,两人互相出题考对方,小月给小东出了这样的一个题目:一个四边形的各个内角度数之比为![]() ,求各个内角的度数.小东想了想,说:“这道题目有问题”.
,求各个内角的度数.小东想了想,说:“这道题目有问题”.
(1)请你指出问题出在哪里;
(2)他们经过研究后,改变题目中的一个数,使这道题没有问题,请你也尝试一下,换一个合适的数,使这道题目没有问题,并进行解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
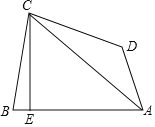
【题目】如图,在四边形ABCD中,AC是四边形的对角线,∠CAD=30°,过点C作CE⊥AB于点E,∠B=2∠BAC,∠ADC﹣∠BAC=90°,若AB=20,CD=16,则BE的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
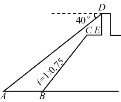
【题目】如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1∶0.75,坡长BC=10米,则此时AB的长约为__米.(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)
查看答案和解析>>
科目:初中数学 来源: 题型:
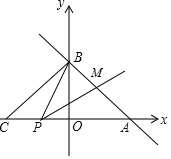
【题目】如图,已知直线y=-![]() x+b与y轴相交于点B(0,3),与x轴交于点A,将△AOB沿y轴折叠,使点A落在x轴上的点C.
x+b与y轴相交于点B(0,3),与x轴交于点A,将△AOB沿y轴折叠,使点A落在x轴上的点C.
(1)求点C的坐标;
(2)设点P为线段CA上的一个动点,点P与点A、C不重合.联结PB.以点P为端点作射线PM交AB于点M,使∠BPM=∠BAC.
①求证:△PBC∽△MPA.
②是否存在点P,使△PBM为直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com