
【题目】我们已经知道,形如![]() 的无理数的化简要借助平方差公式:
的无理数的化简要借助平方差公式:
例如: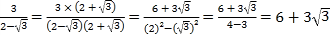 。
。
下面我们来看看完全平方公式在无理数化简中的作用。
问题提出:![]() 该如何化简?
该如何化简?
建立模型:形如![]() 的化简,只要我们找到两个数
的化简,只要我们找到两个数![]() ,使
,使![]() ,这样
,这样![]() ,
,![]() ,那么便有:
,那么便有:![]() ,
,
问题解决:化简![]() ,
,
解:首先把![]() 化为
化为![]() ,这里
,这里![]() ,
,![]() ,由于4+3=7,
,由于4+3=7,![]() ,
,
即(![]() ,
,![]() ,
,
∴![]()
模型应用1:
利用上述解决问题的方法化简下列各式:
(1)![]() ;(2)
;(2)![]() ;
;
模型应用2:
(3)在![]() 中,
中,![]() ,
,![]() ,
,![]() ,那么
,那么![]() 边的长为多少?(结果化成最简)。
边的长为多少?(结果化成最简)。
科目:初中数学 来源: 题型:
【题目】如图,长方体ABCD-A'B'C'D'是个无上底长方体容器,长AB=5cm,宽BC=3cm,高AA′=8cm,甜食点M在容器内侧,位于侧棱BB′的中点,一只蚂蚁从容器外部的A爬到点M处吃甜食,这只蚂蚁爬行的最短路径是( )cm
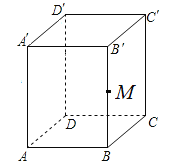
A.![]() B.13C.
B.13C.![]() D.14
D.14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() ,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1B,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x的垂线交直线于点B2, 以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A5的坐标为( )
,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1B,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x的垂线交直线于点B2, 以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A5的坐标为( )
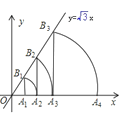
A. (16,0) B. (12,0) C. (8,0) D. (32,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC 是等边三角形,点 P 在△ABC 内,PA=2,将△PAB 绕点 A 逆时针旋转得到△P1AC,则 P1P 的长等于( )

A. 2 B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
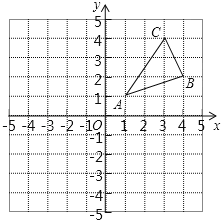
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC关于原点对称的△A1B1C1;
(2)四边形CBC1B1为 四边形;
(3)点P为平面内一点,若以点A、B、C、P为顶点的四边形为平行四边形,请直接写出所有满足条件的点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店用![]() 元采购一批书包,上市后发现供不应求,很快销售完了.商店又去采购第二批同样款式的书包,进货单价比第一次高
元采购一批书包,上市后发现供不应求,很快销售完了.商店又去采购第二批同样款式的书包,进货单价比第一次高![]() 元,商店用了
元,商店用了![]() 元,所购数量是第一次的
元,所购数量是第一次的![]() 倍.
倍.
(1)求第一批采购的书包的单价是多少元?
(2)若商店按售价为每个书包![]() 元,销售完这两批书包,总共获利多少元?
元,销售完这两批书包,总共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
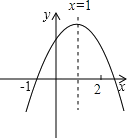
【题目】已知二次函数y=ax2+bx+c的图象如图所示,对称轴为x=1,经过点(-1,0),有下列结论:①abc<0;②a+c>b;③3a+c=0;④a+b>m(am+b)(其中m≠1)其中正确的结论有( )
A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于代数式ax2+bx+c(a≠0),下列说法正确的是( )
①如果存在两个实数p≠q,使得ap2+bp+c=aq2+bq+c,则a![]() +bx+c=a(x-p)(x-q)
+bx+c=a(x-p)(x-q)
②存在三个实数m≠n≠s,使得am2+bm+c=an2+bn+c=as2+bs+c
③如果ac<0,则一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c
④如果ac>0,则一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c
A. ③ B. ①③ C. ②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的图象经过M(1,0)和N(3,0)两点,且与y轴交于D(0,3),直线l是抛物线的对称轴.
(1)求该抛物线的解析式.
(2)若过点A(﹣1,0)的直线AB与抛物线的对称轴和x轴围成的三角形面积为6,求此直线的解析式.
(3)点P在抛物线的对称轴上,⊙P与直线AB和x轴都相切,求点P的坐标.
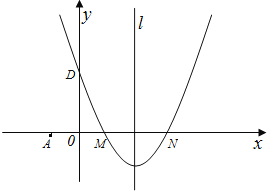
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com