【题目】小月和小东在一起探究有关“多边形内角和”的问题，两人互相出题考对方，小月给小东出了这样的一个题目：一个四边形的各个内角度数之比为
，求各个内角的度数．小东想了想，说：“这道题目有问题”．
（1）请你指出问题出在哪里；
（2）他们经过研究后，改变题目中的一个数，使这道题没有问题，请你也尝试一下，换一个合适的数，使这道题目没有问题，并进行解答．
【答案】（1）见解析；（2）将四边形的各个内角度数之比改为1:2:3:4，四边形的四个内角度数分别为36°，72°，108°，144°
【解析】
（1）设此四边形的四个内角度数为x°、2x°、3x°、6x°，根据四边形的内角和为360°，求出x的值可得最大内角为180°，即可解决问题；
（2）将比值中最大的数减小，类比（1）求解可得．
解：（1）设此四边形的四个内角度数为x°、2x°、3x°、6x°，
则x＋2x＋3x＋6x=360，
解得：x=30，
所以最大的内角度数为6x=180°，
则此多边形不是四边形；
（2）将四边形的各个内角的度数之比为1：2：3：6改为1：2：3：4，
设此四边形的四个内角度数为x°、2x°、3x°、4x°，
则x＋2x＋3x＋4x=360，
解得：x=36，
所以四边形的四个内角度数分别为36°、72°、108°，144°．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】某文化用品商店用
元采购一批书包，上市后发现供不应求，很快销售完了.商店又去采购第二批同样款式的书包，进货单价比第一次高
元，商店用了
元，所购数量是第一次的
倍.
（1）求第一批采购的书包的单价是多少元？
（2）若商店按售价为每个书包
元，销售完这两批书包，总共获利多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
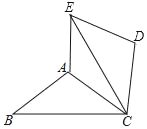
【题目】如图，△ABC中，∠ACB中，∠ACB=30°，将△ABC绕点C顺时针旋转60°得到△DEC，连接AE．
（1）求证：△ABC≌△AEC；
（2）若AB=AC，试判断四边形ACDE的形状，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在实数的计算过程中去发现规律．
（1）5＞2，而
＜
，规律：若a＞b＞0，那么
与
的大小关系是： ．
（2）对于很小的数0.1、0.001、0.00001，它们的倒数
＝ ；
＝ ；
＝ ．规律：当正实数x无限小（无限接近于0），那么它的倒数
．
（3）填空：若实数x的范围是0＜x＜2，写出的范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，抛物线y=ax2+bx+c（a≠0）的图象经过M（1，0）和N（3，0）两点，且与y轴交于D（0，3），直线l是抛物线的对称轴．
（1）求该抛物线的解析式．
（2）若过点A（﹣1，0）的直线AB与抛物线的对称轴和x轴围成的三角形面积为6，求此直线的解析式．
（3）点P在抛物线的对称轴上，⊙P与直线AB和x轴都相切，求点P的坐标．
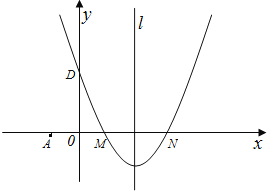
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两人进行羽毛球比赛，羽毛球飞行的路线为抛物线的一部分，如图，甲在
点上正方
的
处发出一球，羽毛球飞行的高度
与水平距离
之间满足函数表达式
．已知点与球网的水平距离为
，球网的高度为
．
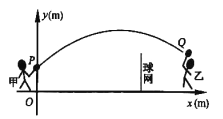
（1）当
时，①求
的值．②通过计算判断此球能否过网．
（2）若甲发球过网后，羽毛球飞行到点的水平距离为
，离地面的高度为
的
处时，乙扣球成功，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
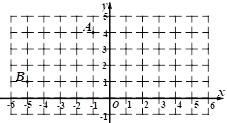
【题目】点A（1,4）和点B（5,1）在平面直角坐标系中的位置如图所示:
（1）点A1、B1分别为点A、B关于y轴的对称点，请画出四边形AA1B1B，并写出A1、B1的坐标;
（2）在（1）的条件下，画一条过四边形AA1B1B的一个顶点的线段，将四边形AA1B1B分成两个图形，并且使分得的图形中的一个是轴对称图形.
查看答案和解析>>
科目：初中数学 来源： 题型：
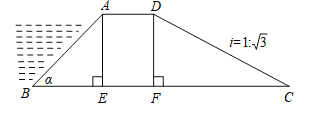
【题目】如图所示，某拦水大坝的横断面为梯形ABCD，AE、DF为梯形的高，其中迎水坡AB的坡角α=45°，坡长AB=
米，背水坡CD的坡度i=1：
（i为DF与FC的比值），则背水坡CD的坡长为______米．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
