【题目】
的三边长分别为
．
求
的取值范围；
当的周长为偶数时，求；
若为等腰三角形，求．
【答案】（1）4＜x＜14；（2）x=6、8、10,12；（3）x=5或9．
【解析】
（1）根据三角形的第三边大于两边之差，而小于两边之和进行计算；
（2）要使周长是偶数，因为其它两边之和是13，则x应是奇数；
（3）根据等腰三角形的定义：有两边相等的三角形是等腰三角形，则x=4或9，再根据（1）中的取值范围进行取舍．
△ABC的三边长分别为5、9、x，
（1）根据三角形的第三边大于两边之差，而小于两边之和，得9-5＜x＜9+5，即4＜x＜14；
（2）因为已知的两边之和是14，为偶数，要使周长为偶数，则第三边应是偶数，即x=6、8、10,12；
（3）若△ABC为等腰三角形，x=5或9．
备战中考寒假系列答案科目：初中数学 来源： 题型：
【题目】勾股定理是几何中的一个重要定理．在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载．如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图2是把图1放入长方形内得到的，
，AB=3，AC=4，点D，E，F，G，H，I都在长方形KLMJ的边上，则长方形KLMJ的面积为___．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小月和小东在一起探究有关“多边形内角和”的问题，两人互相出题考对方，小月给小东出了这样的一个题目：一个四边形的各个内角度数之比为
，求各个内角的度数．小东想了想，说：“这道题目有问题”．
（1）请你指出问题出在哪里；
（2）他们经过研究后，改变题目中的一个数，使这道题没有问题，请你也尝试一下，换一个合适的数，使这道题目没有问题，并进行解答．
查看答案和解析>>
科目：初中数学 来源： 题型：
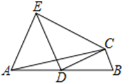
【题目】如图，在△ABC中，点D是线段AB的中点，DC⊥BC，作∠EAB＝∠B，DE∥BC，连接CE．若
，设△BCD的面积为S，则用S表示△ACE的面积正确的是（ ）
A.
B.3S
C.4SD.
查看答案和解析>>
科目：初中数学 来源： 题型：
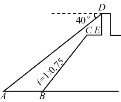
【题目】如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1∶0.75,坡长BC=10米,则此时AB的长约为__米.(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,某武警部队在一次地震抢险救灾行动中,探险队员在相距4米的水平地面A,B两处均探测出建筑物下方C处有生命迹象,已知在A处测得探测线与地面的夹角为30°,在B处测得探测线与地面的夹角为60°,求该生命迹象C所在位置的深度.(结果精确到0.1米,参考数据:
≈1.41,
≈1.73)
查看答案和解析>>
科目：初中数学 来源： 题型：
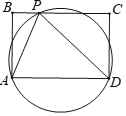
【题目】在矩形ABCD中，AB=4，BC=6，动点P为矩形边上的一点，点P沿着B﹣C的路径运动（含点B和点C），则△ADP的外接圆的圆心O的运动路径长是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如果一个自然数可以表示为两个连续奇数的立方差，那么我们就称这个自然数为“麻辣数”．如：
所以2，26均为“麻辣数”．注：立方差公式
(1)请判断98和169是否为“麻辣数”，并说明理由；
(2)请求出在不超过2016的自然数中，所有的“麻辣数”之和为多少？写出完整的求解过程．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，已知∠ABC=90°，△ABC是等腰三角形，点D为斜边AC的中点，连接DB，过点A作∠BAC的平分线，分别与DB，BC相交于点E，F．
（1）求证：BE=BF；
（2）如图2，连接CE，在不添加任何辅助线的条件下，直接写出图中所有的等腰三角形．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com