
【题目】如图1,已知∠ABC=90°,△ABC是等腰三角形,点D为斜边AC的中点,连接DB,过点A作∠BAC的平分线,分别与DB,BC相交于点E,F.
(1)求证:BE=BF;
(2)如图2,连接CE,在不添加任何辅助线的条件下,直接写出图中所有的等腰三角形.

【答案】(1)见解析;(2)△ABD、△CBD是等腰三角形,△ABC是等腰三角形,△BEF是等腰三角形.
【解析】
(1)根据直角三角形的性质得到BD⊥AC,∠DBC=45°,根据角平分线的定义得到∠BAF=22.5°,根据三角形内角和定理计算,根据等腰三角形的判定定理证明即可;
(2)根据等腰三角形的概念解答.
(1)证明:∠ABC=90°,BA=BC,点D为斜边AC的中点,
∴BD⊥AC,∠DBC=45°,
∵AF是∠BAC的平分线,
∴∠BAF=22.5°,
∴∠BFE=67.5°,
∴∠BEF=180°﹣∠EBF﹣∠EFB=67.5°,
∴∠BFE=∠BEF,
∴BE=BF;
(2)∵∠ABC=90°,BA=BC,点D为斜边AC的中点,
∴BD=AD=CD,
∴△ABD、△CBD是等腰三角形,
由已知得,△ABC是等腰三角形,
由(1)得,△BEF是等腰三角形,
∵AF是∠BAC的平分线,BD是∠ABC的平分线,
∴点E是△ABC的内心,
∴∠EAC=∠ECA=22.5°,
∴△AEC是等腰三角形.


 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
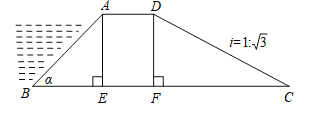
【题目】如图所示,某拦水大坝的横断面为梯形ABCD,AE、DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长AB=![]() 米,背水坡CD的坡度i=1:
米,背水坡CD的坡度i=1:![]() (i为DF与FC的比值),则背水坡CD的坡长为______米.
(i为DF与FC的比值),则背水坡CD的坡长为______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
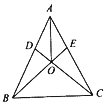
【题目】如图,![]() 中,AB=AC,D、E分别在边AB、AC上,且满足AD=AE.下列结论中:①
中,AB=AC,D、E分别在边AB、AC上,且满足AD=AE.下列结论中:①![]() ;②AO平分∠BAC;③OB=OC;④AO⊥BC;⑤若
;②AO平分∠BAC;③OB=OC;④AO⊥BC;⑤若![]() ,则
,则![]() ;其中正确的有( )
;其中正确的有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,那么△PBQ的面积S随出发时间t(s)如何变化?写出函数关系式及t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.

(1)判断∠D是否是直角,并说明理由.
(2)求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
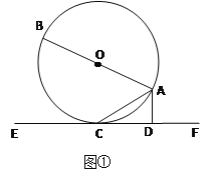
【题目】如图①,AB是⊙O的直径,AC是弦,直线EF和⊙O相切于点C,AD⊥EF,垂足为D。
(1)求证:∠DAC=∠BAC;
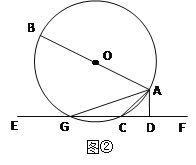
(2)若把直线EF向上平行移动,如图②,EF交⊙O于G、C两点,若题中的其它条件不变,猜想:此时与∠DAC相等的角是哪一个?并证明你的结论。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com