
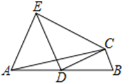
【题目】如图,在△ABC中,点D是线段AB的中点,DC⊥BC,作∠EAB=∠B,DE∥BC,连接CE.若![]() ,设△BCD的面积为S,则用S表示△ACE的面积正确的是( )
,设△BCD的面积为S,则用S表示△ACE的面积正确的是( )
A.![]() B.3S
B.3S
C.4SD.![]()
【答案】C
【解析】
延长AE,BC交于点F,易得AE=DE,由DE∥BC,D为AB的中点,可知DE为中位线,所以BF=2DE,设BC=2x,AE=DE=5x,则BF=10x,CF=BF-BC=8x,在△ABF和△ACF中,分别利用同高的两个三角形面积之比等于底边之比,可推出面积关系.
如图所示,延长AE,BC交于点F
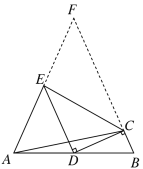
∵DE∥BC,∴∠ADE=∠B,
又∵∠EAB=∠B,∴∠ADE=∠EAB,∴AE=DE
∵D为AB的中点,DE∥BF,∴DE为△ABF的中位线,
∴BF=2DE,
设BC=2x,AE=DE=5x,则BF=10x,CF=BF-BC=8x,
在△ABC中,∵D是AB的中点,∴S△ACD=S△BCD=S
∴S△ABC=2S,
在△ABF中,![]()
∴![]()
在△ACF中,E为AF的中点,
∴![]()
故选C.


科目:初中数学 来源: 题型:
【题目】高尔夫运动员将一个小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间(s)满足二次函数关系,t与h的几组对应值如下表所示:
t(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
h(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在实数的计算过程中去发现规律.
(1)5>2,而![]() <
<![]() ,规律:若a>b>0,那么
,规律:若a>b>0,那么![]() 与
与![]() 的大小关系是:
的大小关系是:![]()
![]() .
.
(2)对于很小的数0.1、0.001、0.00001,它们的倒数![]() = ;
= ;![]() = ;
= ;![]() = .规律:当正实数x无限小(无限接近于0),那么它的倒数
= .规律:当正实数x无限小(无限接近于0),那么它的倒数![]() .
.
(3)填空:若实数x的范围是0<x<2,写出![]() 的范围.
的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
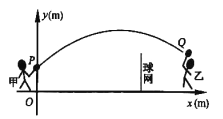
【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在![]() 点上正方
点上正方![]() 的
的![]() 处发出一球,羽毛球飞行的高度
处发出一球,羽毛球飞行的高度![]() 与水平距离
与水平距离![]() 之间满足函数表达式
之间满足函数表达式![]() .已知点
.已知点![]() 与球网的水平距离为
与球网的水平距离为![]() ,球网的高度为
,球网的高度为![]() .
.
(1)当![]() 时,①求
时,①求![]() 的值.②通过计算判断此球能否过网.
的值.②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到点![]() 的水平距离为
的水平距离为![]() ,离地面的高度为
,离地面的高度为![]() 的
的![]() 处时,乙扣球成功,求
处时,乙扣球成功,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
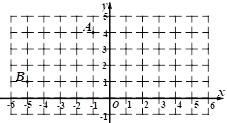
【题目】点A(1,4)和点B(5,1)在平面直角坐标系中的位置如图所示:
(1)点A1、B1分别为点A、B关于y轴的对称点,请画出四边形AA1B1B,并写出A1、B1的坐标;
(2)在(1)的条件下,画一条过四边形AA1B1B的一个顶点的线段,将四边形AA1B1B分成两个图形,并且使分得的图形中的一个是轴对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
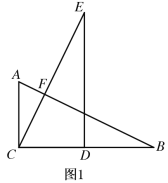
【题目】如图,Rt△ABC≌Rt△CED(∠ACB=∠CDE=90°),点D在BC上,AB与CE相交于点F
(1) 如图1,直接写出AB与CE的位置关系
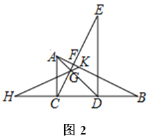
(2) 如图2,连接AD交CE于点G,在BC的延长线上截取CH=DB,射线HG交AB于K,求证:HK=BK
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com