
【题目】在实数的计算过程中去发现规律.
(1)5>2,而![]() <
<![]() ,规律:若a>b>0,那么
,规律:若a>b>0,那么![]() 与
与![]() 的大小关系是:
的大小关系是:![]()
![]() .
.
(2)对于很小的数0.1、0.001、0.00001,它们的倒数![]() = ;
= ;![]() = ;
= ;![]() = .规律:当正实数x无限小(无限接近于0),那么它的倒数
= .规律:当正实数x无限小(无限接近于0),那么它的倒数![]() .
.
(3)填空:若实数x的范围是0<x<2,写出![]() 的范围.
的范围.
【答案】(1)<;(2)10;1000;100000;无穷大;(3)![]() >
>![]()
【解析】
(1)两个正实数,这个数越大,则它的倒数越小,判断出![]() 与
与![]() 的大小关系即可;
的大小关系即可;
(2)首先求出0.1、0.001、0.00001的倒数各是多少;然后判断出当正实数x无限小(无限接近于0),那么它的倒数![]() 无穷大;
无穷大;
(3)根据:0<x<2,可得:![]() >
>![]() .
.
解:(1)5>2,而![]() <
<![]() ,规律:若a>b>0,那么
,规律:若a>b>0,那么![]() 与
与![]() 的大小关系是:
的大小关系是:![]() <
<![]() ,
,
故答案为:<;
(2)对于很小的数0.1、0.001、0.00001,它们的倒数![]() =10;
=10;![]() =1000;
=1000;![]() =100000.
=100000.
规律:当正实数x无限小(无限接近于0),那么它的倒数![]() 无穷大,
无穷大,
故答案为:10; 1000; 100000;无穷大;
(3)∵0<x<2,
∴![]() >
>![]() .
.
故答案为:![]() >
>![]() .
.


科目:初中数学 来源: 题型:
【题目】为了倡导“全民阅读”,某校为调查了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成统计图表如下:
学生家庭藏书情况扇形统计图

类别 | 家庭藏书 | 学生人数 |
|
| 16 |
|
|
|
|
| 50 |
|
| 70 |
根据以上信息,解答下列问题:
(1)共抽样调查了______名学生,![]() ______;
______;
(2)在扇形统计图中,“![]() ”对应扇形的圆心角为_______
”对应扇形的圆心角为_______![]() ;
;
(3)若该校有2000名学生,请估计全校学生中家庭藏书超过60本的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是把图1放入长方形内得到的,![]() ,AB=3,AC=4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为___.
,AB=3,AC=4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(单位:分):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4 分 2,则成绩较为整齐的是 队.
查看答案和解析>>
科目:初中数学 来源: 题型:
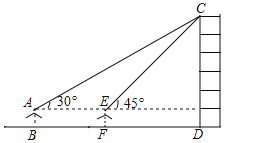
【题目】(7分)小敏同学测量一建筑物CD的高度,她站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走30m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据:![]() ,
,![]() .结果保留整数)
.结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2).
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小月和小东在一起探究有关“多边形内角和”的问题,两人互相出题考对方,小月给小东出了这样的一个题目:一个四边形的各个内角度数之比为![]() ,求各个内角的度数.小东想了想,说:“这道题目有问题”.
,求各个内角的度数.小东想了想,说:“这道题目有问题”.
(1)请你指出问题出在哪里;
(2)他们经过研究后,改变题目中的一个数,使这道题没有问题,请你也尝试一下,换一个合适的数,使这道题目没有问题,并进行解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
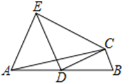
【题目】如图,在△ABC中,点D是线段AB的中点,DC⊥BC,作∠EAB=∠B,DE∥BC,连接CE.若![]() ,设△BCD的面积为S,则用S表示△ACE的面积正确的是( )
,设△BCD的面积为S,则用S表示△ACE的面积正确的是( )
A.![]() B.3S
B.3S
C.4SD.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个自然数可以表示为两个连续奇数的立方差,那么我们就称这个自然数为“麻辣数”.如:![]() 所以2,26均为“麻辣数”.注:立方差公式
所以2,26均为“麻辣数”.注:立方差公式![]()
(1)请判断98和169是否为“麻辣数”,并说明理由;
(2)请求出在不超过2016的自然数中,所有的“麻辣数”之和为多少?写出完整的求解过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com