练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

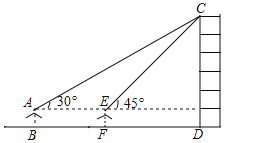
    【题目】（7分）小敏同学测量一建筑物CD的高度，她站在B处仰望楼顶C，测得仰角为30°，再往建筑物方向走30m，到达点F处测得楼顶C的仰角为45°（BFD在同一直线上）．已知小敏的眼睛与地面距离为1.5m，求这栋建筑物CD的高度（参考数据：，．结果保留整数）

    【答案】42．

    【解析】

    试题延长AE交CD于点G，设CG=xm，在Rt△CGE中利用x表示出EG，在Rt△ACG中，利用x表示出AG，根据AE=AG﹣EG即可列方程求得x的值，进而球儿CD的长．

    试题解析：延长AE交CD于点G．设CG=xm，在直角△CGE中，∠CEG=45°，则EG=CG=xm．在直角△ACG中，AG==m．∵AG﹣EG=AE，∴，解得：x=≈15×2.732≈40.98（m）．则CD=40.98+1.5=42.48（m）．

    答：这栋建筑物CD的高度约为42m．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】△ABC 是等边三角形，点 P 在△ABC 内，PA=2，将△PAB 绕点 A 逆时针旋转得到△P1AC，则 P1P 的长等于（ ）

    A. 2 B. C. D. 1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于代数式ax2+bx+c(a≠0)，下列说法正确的是（ ）

    ①如果存在两个实数p≠q，使得ap2+bp+c=aq2+bq+c，则a+bx+c=a（x-p）（x-q）

    ②存在三个实数m≠n≠s，使得am2+bm+c=an2+bn+c=as2+bs+c

    ③如果ac＜0，则一定存在两个实数m＜n，使am2+bm+c＜0＜an2+bn+c

    ④如果ac＞0，则一定存在两个实数m＜n，使am2+bm+c＜0＜an2+bn+c

    A. ③ B. ①③ C. ②④ D. ①③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

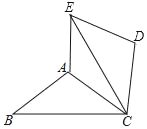
    【题目】如图，△ABC中，∠ACB中，∠ACB=30°，将△ABC绕点C顺时针旋转60°得到△DEC，连接AE．

    （1）求证：△ABC≌△AEC；

    （2）若AB=AC，试判断四边形ACDE的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知直线AC的表达式为y＝x＋8，点P从点A开始沿AO向点O以1个单位/s的速度移动，点Q从点O开始沿OC向点C以2个单位/s的速度移动．如果P，Q两点分别从点A，O同时出发，经过几秒能使△PQO的面积为8个平方单位？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在实数的计算过程中去发现规律．

    （1）5＞2，而＜，规律：若a＞b＞0，那么与的大小关系是：　 　．

    （2）对于很小的数0.1、0.001、0.00001，它们的倒数＝　 　；＝　 　；＝　 　．规律：当正实数x无限小（无限接近于0），那么它的倒数　 　．

    （3）填空：若实数x的范围是0＜x＜2，写出的范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，抛物线y=ax2+bx+c（a≠0）的图象经过M（1，0）和N（3，0）两点，且与y轴交于D（0，3），直线l是抛物线的对称轴．

    （1）求该抛物线的解析式．

    （2）若过点A（﹣1，0）的直线AB与抛物线的对称轴和x轴围成的三角形面积为6，求此直线的解析式．

    （3）点P在抛物线的对称轴上，⊙P与直线AB和x轴都相切，求点P的坐标．

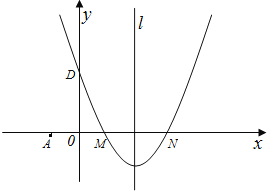
    查看答案和解析>>

    科目：初中数学 来源： 题型：

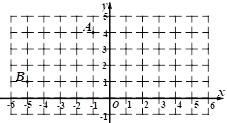
    【题目】点A（1,4）和点B（5,1）在平面直角坐标系中的位置如图所示:

    （1）点A1、B1分别为点A、B关于y轴的对称点，请画出四边形AA1B1B，并写出A1、B1的坐标;

    （2）在（1）的条件下，画一条过四边形AA1B1B的一个顶点的线段，将四边形AA1B1B分成两个图形，并且使分得的图形中的一个是轴对称图形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知正方形ABCD中，BE平分∠DBC且交CD边于点E，将△BCE绕点C顺时针旋转到△DCF的位置，并延长BE交DF于点G．

    （1）求证：△BDG∽△DEG；

    （2）若EGBG=4，求BE的长．

    查看答案和解析>>

    同步练习册答案