
【题目】如图,△ABC中,∠ACB中,∠ACB=30°,将△ABC绕点C顺时针旋转60°得到△DEC,连接AE.
(1)求证:△ABC≌△AEC;
(2)若AB=AC,试判断四边形ACDE的形状,并说明理由.
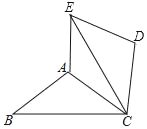
【答案】(1)见解析;(2)四边形ACDE是菱形.理由见解析.
【解析】
(1)根据旋转的性质得出BC=EC,∠ACB=∠DCE=30°,∠BCE=60°,那么∠ACE=30°=∠ACB.再根据SAS即可证明△ABC≌△AEC;
(2)由(1)得△ABC≌△AEC,那么AE=AB,而AB=AC,等量代换得出AE=AB=AC.根据旋转的性质得出△DEC≌△ABC,那么CD=AC=AB,DE=AB,从而得出AC=CD=DE=AE,进而得到四边形ACDE是菱形.
(1)证明:∵将△ABC绕点C顺时针旋转60°得到△DEC,
∴BC=EC,∠ACB=∠DCE=30°,∠BCE=60°,
∴∠ACE=60°﹣30°=30°,
∴∠ACE=∠ACB.
在△ABC与△AEC中,
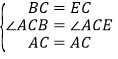
∴△ABC≌△AEC(SAS);
(2)解:四边形ACDE是菱形.理由如下:
由(1)得△ABC≌△AEC,
∴AE=AB,
∴AB=AC,
∴AE=AB=AC.
∵△DEC是由△ABC旋转而得,
∴△DEC≌△ABC,
∴CD=AC=AB,DE=AB,
∴AC=CD=DE=AE,
∴四边形ACDE是菱形.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )

A.带①去B.带②去C.带③去D.带①和②去
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 11 | 6 | 3 | 2 | 3 | … |
则当y≤6时x的取值范围是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是把图1放入长方形内得到的,![]() ,AB=3,AC=4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为___.
,AB=3,AC=4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,动点E、F分别从D、C两点同时出发,以相同的速度分别在边DC、CB上移动,当点E运动到点C时都停止运动,DF与AE相交于点P,若AD=8,则点P运动的路径长为( )

A. 8![]() B. 4
B. 4![]() C. 4π D. 2π
C. 4π D. 2π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(单位:分):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4 分 2,则成绩较为整齐的是 队.
查看答案和解析>>
科目:初中数学 来源: 题型:
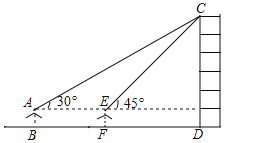
【题目】(7分)小敏同学测量一建筑物CD的高度,她站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走30m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据:![]() ,
,![]() .结果保留整数)
.结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小月和小东在一起探究有关“多边形内角和”的问题,两人互相出题考对方,小月给小东出了这样的一个题目:一个四边形的各个内角度数之比为![]() ,求各个内角的度数.小东想了想,说:“这道题目有问题”.
,求各个内角的度数.小东想了想,说:“这道题目有问题”.
(1)请你指出问题出在哪里;
(2)他们经过研究后,改变题目中的一个数,使这道题没有问题,请你也尝试一下,换一个合适的数,使这道题目没有问题,并进行解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=4,BC=6,动点P为矩形边上的一点,点P沿着B﹣C的路径运动(含点B和点C),则△ADP的外接圆的圆心O的运动路径长是_____.
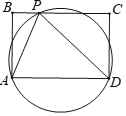
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com