
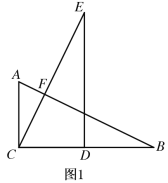
【题目】如图,Rt△ABC≌Rt△CED(∠ACB=∠CDE=90°),点D在BC上,AB与CE相交于点F
(1) 如图1,直接写出AB与CE的位置关系
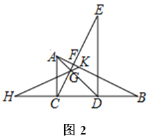
(2) 如图2,连接AD交CE于点G,在BC的延长线上截取CH=DB,射线HG交AB于K,求证:HK=BK
【答案】(1)AB⊥CE;(2)见解析.
【解析】
(1)由全等可得∠ECD=∠A,再由∠B+∠A=90°,可得∠B+ECD=90°,则AB⊥CE.
(2)延长HK于DE交于H,易得△ACD为等腰直角三角形,∠ADC=45°,易得DH=DE,然后证明△DGH≌△DGE,所以∠H=∠E,则∠H=∠B,可得HK=BK.
解:(1)∵Rt△ABC≌Rt△CED,
∴∠ECD=∠A,∠B=∠E,BC=DE,AC=CD
∵∠B+∠A=90°
∴∠B+ECD=90°
∴∠BFC=90°,∴AB⊥CE
(2)在Rt△ACD中,AC=CD,∴∠ADC=45°,
又∵∠CDE=90°,∴∠HDG=∠CDG=45°
∵CH=DB,∴CH+CD=DB+CD,即HD=BC,
∴DH=DE,
在△DGH和△DGE中,
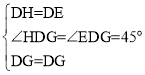
∴△DGH≌△DGE(SAS)
∴∠H=∠E
又∵∠B=∠E
∴∠H=∠B,
∴HK=BK


科目:初中数学 来源: 题型:
【题目】在等腰Rt△ABC中,AB=AC,∠BAC=90°
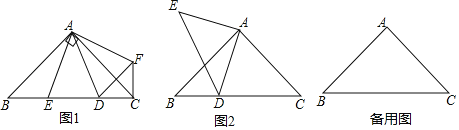
(1)如图1,D,E是等腰Rt△ABC斜边BC上两动点,且∠DAE=45°,将△ABE绕点A逆时针旋转90后,得到△AFC,连接DF
①求证:△AED≌△AFD;
②当BE=3,CE=7时,求DE的长;
(2)如图2,点D是等腰Rt△ABC斜边BC所在直线上的一动点,连接AD,以点A为直角顶点作等腰Rt△ADE,当BD=3,BC=9时,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2).
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AC=BC,点D在△ABC外部,且∠ACB+∠ADB=180°,连接AB、CD.
(1)如图1,当∠ACB=90°时,则∠ADC=______°.
(2)如图2,当∠ACB=60°时,求证:DC平分∠ADB.

查看答案和解析>>
科目:初中数学 来源: 题型:
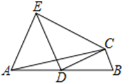
【题目】如图,在△ABC中,点D是线段AB的中点,DC⊥BC,作∠EAB=∠B,DE∥BC,连接CE.若![]() ,设△BCD的面积为S,则用S表示△ACE的面积正确的是( )
,设△BCD的面积为S,则用S表示△ACE的面积正确的是( )
A.![]() B.3S
B.3S
C.4SD.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
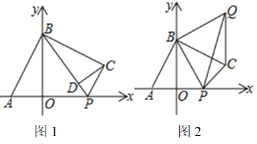
【题目】已知:如图,在平面直角坐标系中,A(a,0)、B(0,b),且|a+2|+(b+2a)2=0,点P为x轴上一动点,连接BP,在第一象限内作BC⊥AB且BC=AB
(1) 求点A、B的坐标
(2) 如图1,连接CP.当CP⊥BC时,作CD⊥BP于点D,求线段CD的长度
(3) 如图2,在第一象限内作BQ⊥BP且BQ=BP,连接PQ.设P(p,0),直接写出S△PCQ=_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某武警部队在一次地震抢险救灾行动中,探险队员在相距4米的水平地面A,B两处均探测出建筑物下方C处有生命迹象,已知在A处测得探测线与地面的夹角为30°,在B处测得探测线与地面的夹角为60°,求该生命迹象C所在位置的深度.(结果精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
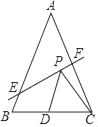
【题目】如图,△ABC的面积是12,AB=AC,BC=3,边AC的垂直平分线交AC于F,交AB于E.点D是BC的中点,点P是EF上的一个动点,则△PCD的周长最小值是( )
A.4B.8C.7D.9.5
查看答案和解析>>
科目:初中数学 来源: 题型:
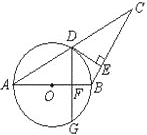
【题目】如图,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E.
(1)求证:DE是⊙O的切线;
(2)作DG⊥AB交⊙O于G,垂足为F,若∠A=30°,AB=8,求弦DG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com