
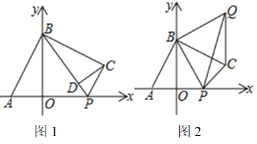
【题目】已知:如图,在平面直角坐标系中,A(a,0)、B(0,b),且|a+2|+(b+2a)2=0,点P为x轴上一动点,连接BP,在第一象限内作BC⊥AB且BC=AB
(1) 求点A、B的坐标
(2) 如图1,连接CP.当CP⊥BC时,作CD⊥BP于点D,求线段CD的长度
(3) 如图2,在第一象限内作BQ⊥BP且BQ=BP,连接PQ.设P(p,0),直接写出S△PCQ=_____
【答案】(1)A(-2,0),B(0,4);(2)CD=2;(3)![]()
【解析】
(1)由非负数的性质,可求出a、b的值,得到A、B的坐标;
(2)过C作CE⊥OB于E,与PB交于F,易证△AOB≌△BEC,可得OA=BE=2,即E为OB中点,所以EF为△BOP的中位线,F为Rt△BCP斜边BP上的中点,所以![]() ,所以∠BCF=∠CBD=∠ABO,再证△AOB≌△CDB即可得CD=OA.
,所以∠BCF=∠CBD=∠ABO,再证△AOB≌△CDB即可得CD=OA.
(3)过B作BG⊥CQ于点G,延长QC与x轴交于H,通过证△ABP≌△CBQ,△BOP≌△BGQ可推出OBGH为矩形,以CQ为底,PH为高求面积.
解:(1)∵|a+2|+(b+2a)2=0
∴a+2=0,b+2a=0,解得a=-2,b=4,
∴A(-2,0),B(0,4)
(2)如图所示,过C作CE⊥OB于E,与PB交于F,
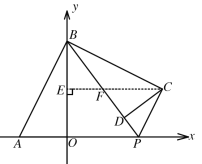
∵BC⊥AB,∴∠ABO+∠EBC=90°,
在Rt△BCE中,∠EBC+∠BCE=90°,
∴∠ABO=∠BCE
在△AOB和△BEC中,
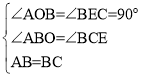
∴△AOB≌△BEC(AAS)
∴BE=AO=2,又∵OB=4,∴E为OB的中点,
∵EC∥OP,∴EF为△BOP的中位线,则F为BP的中点,
在Rt△BCP中,CF为斜边上的中线,
∴![]()
∴∠BCE=∠CBD=∠ABO
在△AOB和△CDB中
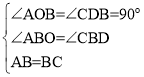
∴△AOB≌△CDB(AAS)
∴CD=AO=2
(3)如下图所示,过B作BG⊥CQ于点G,延长QC与x轴交于H,

∵∠ABP+∠PBC=90°,∠PBC+CBQ=90°,
∴∠ABP=∠CBQ
在△ABP与△CBQ中,
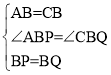
∴△ABP≌△CBQ(SAS)
∴∠BPO=∠BQG,CQ=AP=2+p,
在△BOP和△BGQ中,
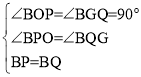
∴△BOP≌△BGQ(AAS)
∴∠OBP=∠GBQ,BG=BO=4
又∵∠GBQ+∠PBG=90°
∴∠OBP+∠PBG=90°,即∠OBG=90°,
在四边形OBGH中,∠OBG=∠BOG=∠BGH=90°,
∴∠OHG=90°,∴PH是△PCQ中CQ边上的高,
PH=OH-OP=4-p
∴![]()


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=2x+6与x轴交于点A,与y轴交于点B,过点B的直线交x轴于点C,且AB=BC.
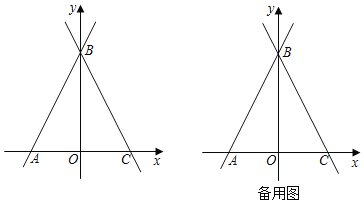
(1)求直线BC的解析式;
(2)点P为线段AB上一点,点Q为线段BC延长线上一点,且AP=CQ,设点Q横坐标为m,求点P的坐标(用含m的式子表示,不要求写出自变量m的取值范围);
(3)在(2)的条件下,点M在y轴负半轴上,且MP=MQ,若∠BQM=45°,求直线PQ的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AB∥CD,AB=14,AD= 4![]() , CD=7.直线l经过A,D两点,且sin∠DAB=
, CD=7.直线l经过A,D两点,且sin∠DAB=![]() . 动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于AB,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
. 动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于AB,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
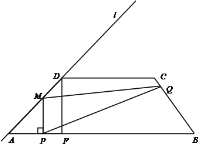
(1)求腰BC的长;
(2)当Q在BC上运动时,求S与t的函数关系式;
(3)在(2)的条件下,是否存在某一时刻t,使得△MPQ的面积S是梯形ABCD面积的![]() ?若存在,请求出t的值;若不存在,请说明理由;
?若存在,请求出t的值;若不存在,请说明理由;
(4)随着P,Q两点的运动,当点M在线段DC上运动时,设PM的延长线与直线l相交于点N,试探究:当t为何值时,△QMN为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M,N分别是AE,CD的中点。试探索BM和BN的关系,并证明你的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
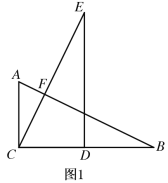
【题目】如图,Rt△ABC≌Rt△CED(∠ACB=∠CDE=90°),点D在BC上,AB与CE相交于点F
(1) 如图1,直接写出AB与CE的位置关系
(2) 如图2,连接AD交CE于点G,在BC的延长线上截取CH=DB,射线HG交AB于K,求证:HK=BK
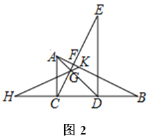
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年某市水果大丰收,![]() 两个水果基地分别收获同种水果
两个水果基地分别收获同种水果![]() 件、
件、![]() 件,现需把这些水果全部运往甲、乙两销售点,从
件,现需把这些水果全部运往甲、乙两销售点,从![]() 基地运往甲、乙两销售点的费用分别为每件
基地运往甲、乙两销售点的费用分别为每件![]() 元和
元和![]() 元,从
元,从![]() 基地运往甲、乙两销售点的费用分别为每件
基地运往甲、乙两销售点的费用分别为每件![]() 元和
元和![]() 元,现甲销售点需要水果
元,现甲销售点需要水果![]() 件,乙销售点需要水果
件,乙销售点需要水果![]() 件.
件.
![]() 设从
设从![]() 基地运往甲销售点水果
基地运往甲销售点水果![]() 件,总运费为
件,总运费为![]() 元,请用含的
元,请用含的![]() 代数式表示
代数式表示![]() ,并写出
,并写出![]() 的取值范围;
的取值范围;
![]() 若总运费不超过
若总运费不超过![]() 元,且
元,且![]() 基地运往甲销售点的水果不低于
基地运往甲销售点的水果不低于![]() 件,试确定运费最低的运输方案,并求出最低运费.
件,试确定运费最低的运输方案,并求出最低运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地,两人之间的距离![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系如图所示,则下列说法正确的是( )
(分钟)之间的函数关系如图所示,则下列说法正确的是( )
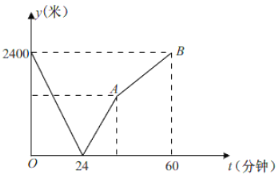
①当![]() 分钟时甲乙两人相遇;
分钟时甲乙两人相遇;
②甲的速度为40米/分钟;
③乙的速度为50米/分钟;
④乙到达目的地时,甲离目的地的距离为800米.
A.①②B.③④C.①②④D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据重庆轨道集团提供的日客运量统计,2019年2月21日重庆轨道交通首次日客运量突破300万乘次,其中近期开通的重庆轨道交通环线日客运量为21.5万乘次.据了解,某工作日上午7点至9点轨道环线四公里站有20列列车进出站,每列车进出站时,将上车和下车的人数记录下来,各得到20个数据,并将数据进行整理,绘制成了如下两幅不完整统计图.(数据分组为:![]() 组:
组:![]() ,
,![]() 组:
组:![]() ,
,![]() 组:
组:![]() ,
,![]() 组:
组:![]() ,
,![]() 组:
组:![]() )
)
I.上车人数在![]() 组的是:190,190,191,192,193,193,195,196,198,198,198,198;
组的是:190,190,191,192,193,193,195,196,198,198,198,198;
II.上车人数的平均数、中位数如下表:
平均数 | 中位数 | |
上车人数(人) | 194 | a |
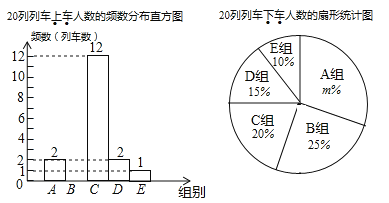
根据以上信息,回答下列问题:
(1)请补全频数分布直方图;
(2)表中![]() ________,扇形统计图中
________,扇形统计图中![]() _________,扇形统计图中
_________,扇形统计图中![]() 组所在的圆心角度数为________度;
组所在的圆心角度数为________度;
(3)请利用平均数,估算一周内5个工作日的上午7点至9点重庆轨道环线四公里站的上车总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,∠BAD+∠BCD=180°, AC平分∠BAD,过点C作CE⊥AD,垂足为E, CD=4,AE=10,则四边形ABCD的周长是____________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com