
【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M,N分别是AE,CD的中点。试探索BM和BN的关系,并证明你的结论。

【答案】BM⊥BN.见解析
【解析】试题分析:根据SAS推出△ABE≌△DBC,推出AE=DC,∠EAB=∠BDC,∠AEB=∠DCB,求出∠ABD=∠DBC=90°,BM=AM=EM=![]() AE,BN=CN=DN=
AE,BN=CN=DN=![]() CD,推出∠ABM=∠DBN,∠EBM=∠NBC即可.
CD,推出∠ABM=∠DBN,∠EBM=∠NBC即可.
解:BM=BN,BM⊥BN,
理由是:在△ABE和△DBC中,
 ,
,
∴△ABE≌△DBC(SAS),
∴AE=DC,∠EAB=∠BDC,∠AEB=∠DCB,
∵∠ABD=∠DBC,∠ABD+∠DBC=180°,
∴∠ABD=∠DBC=90°,
∵M为AE的中点,N为CD的中点,
∴BM=AM=EM=![]() AE,BN=CN=DN=
AE,BN=CN=DN=![]() CD,
CD,
∴BM=BN,∠EAB=∠MBA,∠CDB=∠DBN,∠AEB=∠EBM,∠NCB=∠NBC,
∵∠EAB=∠BDC,∠AEB=∠DCB,
∴∠ABM=∠DBN,∠EBM=∠NBC,
∴∠ABC=2∠DBN+2∠EBM=180°,
∴∠EBN+∠EBM=90°,
∴BM⊥BN.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
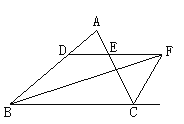
【题目】如图所示:∠ABC的平分线BF与△ABC中∠ACB的相邻外角的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E.
问:(1)图中有几个等腰三角形?为什么?
(2)BD,CE,DE之间存在着什么关系?请证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016湖南省岳阳市第24题)如图①,直线y=![]() x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
(1)求抛物线F1所表示的二次函数的表达式;
(2)若点M是抛物线F1位于第二象限图象上的一点,设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC,记S=S四边形MAOC﹣S△BOC,求S最大时点M的坐标及S的最大值;
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2,点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
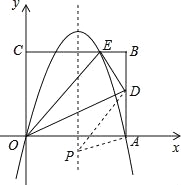
【题目】(2016广西省贺州市第26题)如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标为(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,E点坐标为(6,8),抛物线y=ax2+bx+c经过O、A、E三点.
(1)求此抛物线的解析式;
(2)求AD的长;
(3)点P是抛物线对称轴上的一动点,当△PAD的周长最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
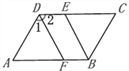
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC的平分线交CD于点E.
(1)若∠A=70°,求∠ABE的度数;
(2)若AB∥CD,且∠1=∠2,判断DF和BE是否平行,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com