
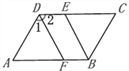
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC的平分线交CD于点E.
(1)若∠A=70°,求∠ABE的度数;
(2)若AB∥CD,且∠1=∠2,判断DF和BE是否平行,并说明理由.
【答案】(1)∠ABE=55°;(2)证明见解析
【解析】试题分析:(1)由平行线的性质可求得∠ ABC =110°,由角平分线的定义可求得∠ABE=55°;(2)DF∥BE,理由:由AB∥ CD,根据平行线的性质可得∠A+∠ADC=180°,∠2=∠AFD,再由AD∥ BC,根据平行线的性质可得∠A+∠ABC=180°,所以∠ADC=∠ABC,再由∠1=∠2=![]() ∠ADC,∠ABE=
∠ADC,∠ABE=![]() ∠ABC,可得∠2=∠ABE,所以∠AFD =∠ABE,即可判定DF∥BE.
∠ABC,可得∠2=∠ABE,所以∠AFD =∠ABE,即可判定DF∥BE.
试题解析:
(1)解:∵AD∥BC,∠A=70°
∴∠ ABC=180°-∠ A=110°
∵BE平分∠ABC
∴∠ABE=![]() ∠ABC=55°
∠ABC=55°
(2)证明:DF∥BE
∵AB∥ CD
∴∠A+∠ADC=180°,∠2=∠AFD
∵AD∥ BC
∴∠A+∠ABC=180°
∴∠ADC=∠ABC
∵∠1=∠2=![]() ∠ADC,∠ABE=
∠ADC,∠ABE=![]() ∠ABC
∠ABC
∴∠2=∠ABE
∴∠AFD =∠ABE
∴DF∥BE


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:初中数学 来源: 题型:
【题目】雅丽服装厂童装车间有40名工人,缝制一种儿童套装(一件上衣和两条裤子配成一套)。已知1名工人一天可缝制童装上衣3件或裤子4件,问怎样分配工人才能使缝制出来的上衣和裤子恰好配套?
查看答案和解析>>
科目:初中数学 来源: 题型:
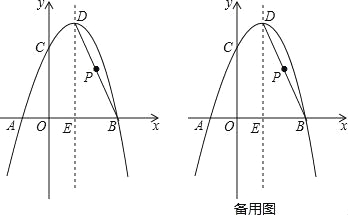
【题目】(2016广东省茂名市第25题)如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线的对称轴DE交x轴于点E,连接BD.
(1)求经过A,B,C三点的抛物线的函数表达式;
(2)点P是线段BD上一点,当PE=PC时,求点P的坐标;
(3)在(2)的条件下,过点P作PF⊥x轴于点F,G为抛物线上一动点,M为x轴上一动点,N为直线PF上一动点,当以F、M、G为顶点的四边形是正方形时,请求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M,N分别是AE,CD的中点。试探索BM和BN的关系,并证明你的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016山西省第23题)综合与探究
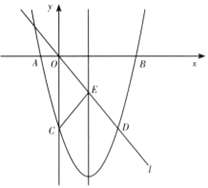
如图,在平面直角坐标系中,已知抛物线![]() 与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0),(6,-8).
与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0),(6,-8).
(1)求抛物线的函数表达式,并分别求出点B和点E的坐标;
(2)试探究抛物线上是否存在点F,使![]() ≌
≌![]() ,若存在,请直接写出点F的坐标;若不存在,请说明理由;
,若存在,请直接写出点F的坐标;若不存在,请说明理由;
(3)若点P是y轴负半轴上的一个动点,设其坐标为(0,m),直线PB与直线l交于点Q.试探究:当m为何值时,![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com