
����Ŀ��(2016ɽ��ʡ��23��)�ۺ���̽��
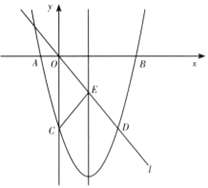
��ͼ����ƽ��ֱ������ϵ�У���֪������![]() ��x�ύ��A��B���㣬��y�ύ�ڵ�C��ֱ��l��������ԭ��O���������ߵ�һ������ΪD���������ߵĶԳ��ύ�ڵ�E������CE����֪��A��D������ֱ�Ϊ����2��0������6����8����
��x�ύ��A��B���㣬��y�ύ�ڵ�C��ֱ��l��������ԭ��O���������ߵ�һ������ΪD���������ߵĶԳ��ύ�ڵ�E������CE����֪��A��D������ֱ�Ϊ����2��0������6����8����
��1���������ߵĺ�������ʽ�����ֱ������B�͵�E�����ꣻ
��2����̽�����������Ƿ���ڵ�F��ʹ![]() ��
��![]() �������ڣ���ֱ��д����F�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ���ֱ��д����F�����ꣻ�������ڣ���˵�����ɣ�
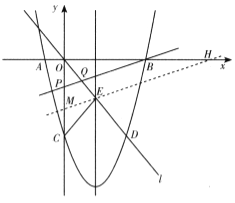
��3������P��y�Ḻ�����ϵ�һ�����㣬��������Ϊ��0��m����ֱ��PB��ֱ��l���ڵ�Q����̽������mΪ��ֵʱ��![]() �ǵ��������Σ�
�ǵ��������Σ�
���𰸡�(1)��![]() ��B(8,0)��E(3��-4)��(2)����
��B(8,0)��E(3��-4)��(2)����![]() ����
����![]() ����(3)��
����(3)��![]() ��
��![]() .
.
��������
���������(1)����A��D��������뺯������ʽ�����Ԫһ�η��̼��������������ʽ����B���꣺���������߶Գ��ԣ�����Գ�����A�����꼴�����B�����ꣻ��E���꣺EΪֱ��l�������߶Գ���Ľ��㣬����D���������l����ʽ�����������Ϊ![]() �����������E�����ꣻ(2)������ȫ�ȶ�Ӧ����ȣ���֪FO=FC�����Ե�F�϶���OC�Ĵ�ֱƽ�����ϣ����Ե�F��������Ϊ-4�����������߱���ʽ��������������ꣻ(3)�����ݵ�P��y�Ḻ�������˶�����������������ۣ��ٽ���������.
�����������E�����ꣻ(2)������ȫ�ȶ�Ӧ����ȣ���֪FO=FC�����Ե�F�϶���OC�Ĵ�ֱƽ�����ϣ����Ե�F��������Ϊ-4�����������߱���ʽ��������������ꣻ(3)�����ݵ�P��y�Ḻ�������˶�����������������ۣ��ٽ���������.
�����������1��![]() ������
������![]() ������A����2��0����D��6����8����
������A����2��0����D��6����8����
![]() ���
���![]()
![]() �����ߵĺ�������ʽΪ
�����ߵĺ�������ʽΪ![]()
![]()
![]() ��
��![]() �����ߵĶԳ���Ϊֱ��
�����ߵĶԳ���Ϊֱ��![]() ����
����![]() ��������x�ύ��A��B���㣬��A������Ϊ����2��0����
��������x�ύ��A��B���㣬��A������Ϊ����2��0����![]() ��B������Ϊ��8��0��
��B��������8��0��
��ֱ��l�ĺ�������ʽΪ![]() ��
��![]() ��D��6����8����ֱ��l�ϣ�
��D��6����8����ֱ��l�ϣ�![]() 6k=��8�����
6k=��8�����![]() ��
��
![]() ֱ��l�ĺ�������ʽΪ
ֱ��l�ĺ�������ʽΪ![]()
![]() ��EΪֱ��l�������߶Գ���Ľ��㣮
��EΪֱ��l�������߶Գ���Ľ��㣮![]() ��E�ĺ�����Ϊ3��������Ϊ
��E�ĺ�����Ϊ3��������Ϊ![]() ��
��
����E��������3����4��
(2)���������ϴ��ڵ�F��ʹ![]() ��
��![]() ����F��������
����F��������![]() ����
����![]() ��
��
(3)�������������
����![]() ʱ��
ʱ��![]() �ǵ��������Σ�
�ǵ��������Σ�
![]() ��E��������3����4����
��E������Ϊ��3����4����![]() ������E��ֱ��ME//PB����y���ڵ�M����x���ڵ�H����
������E��ֱ��ME//PB����y���ڵ�M����x���ڵ�H����![]() ��
��![]()
![]() ��M��������0����5����
��M��������0����5����
��ֱ��ME�ı���ʽΪ![]() ��
��![]()
![]() �����
�����![]() ��
��![]() ME�ĺ�������ʽΪ
ME�ĺ�������ʽΪ![]() ����y=0����
����y=0����![]() �����x=15��
�����x=15��![]() ��H��������15��0��
��H��������15��0��
��![]() MH//PB��
MH//PB��![]()
![]() ����
����![]() ��
��![]()
![]()
����![]() ʱ��
ʱ��![]() �ǵ��������Σ� ��x=0ʱ��
�ǵ��������Σ� ��x=0ʱ��![]() ��
��![]() ��C��������0����8����
��C��������0����8����
![]()
![]() ��
��![]() OE=CE��
OE=CE��![]()
![]() ������Ϊ
������Ϊ![]() ��
��![]()
![]() ��
�� ![]()
![]() ��
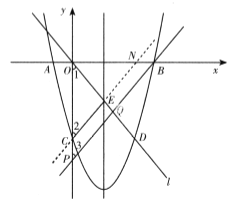
��![]() CE//PB
CE//PB
��ֱ��CE��x���ڵ�N���亯������ʽΪ![]() ��
��![]()
![]() �����
�����![]() ��
��
![]() CE�ĺ�������ʽΪ
CE�ĺ�������ʽΪ![]() ����y=0����
����y=0����![]() ��
��![]()
![]() ��
��![]() ��N��������6��0��
��N��������6��0��
![]() CN//PB��
CN//PB��![]()
![]() ��
��![]()
![]() �����
�����![]()
������������m��ֵΪ![]() ��
��![]() ʱ��
ʱ��![]() �ǵ��������Σ�
�ǵ��������Σ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c��������ABC�����ߣ���b2+2ab=c2+2ac����������ABC����״�������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
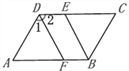
����Ŀ����ͼ�����ı���ABCD�У�AD��BC����ABC��ƽ���߽�CD�ڵ�E.
��1������A=70�㣬���ABE�Ķ�����
��2����AB��CD���ҡ�1=��2���ж�DF��BE�Ƿ�ƽ�У���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��CD����G��E��F�ֱ���AB��CD�ϣ�FGƽ����CFE������1=40��������FGE�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����|a+3|+|b��2|=0����ab��ֵΪ��������
A. ��6 B. ��9 C. 9 D. 6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��֪C��AB���е�,D��AC���е�,E��BC���е�.
(1)��AB=18cm,��DE�ij�;(2)��CE=5cm,��DB�ij�.
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(2016�㶫ʡ�����е�23��)��ͼ��������![]() ��
��![]() �ύ��A��B���㣬��B��1 , 0����
�ύ��A��B���㣬��B��1 , 0����
(1)���������ߵĽ���ʽ�͵�A�����ꣻ
(2)����ͼ1����P��ֱ��![]() �ϵĶ��㣬��ֱ��
�ϵĶ��㣬��ֱ��![]() ƽ����APBʱ�����P�����ꣻ
ƽ����APBʱ�����P�����ꣻ
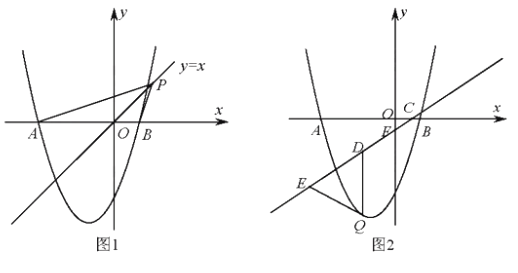
��3����ͼ2����ֱ֪��![]() �ֱ���
�ֱ���![]() ��
�� ![]() �� ����C��F���㡣��Q��ֱ��CF�·����������ϵ�һ�����㣬����Q��
�� ����C��F���㡣��Q��ֱ��CF�·����������ϵ�һ�����㣬����Q�� ![]() ���ƽ���ߣ���ֱ��CF�ڵ�D����E���߶�CD���ӳ����ϣ�����QE������QDΪ���ĵ�����QDE������Ƿ�������ֵ�������ڣ������������ֵ���������ڣ���˵�����ɡ�
���ƽ���ߣ���ֱ��CF�ڵ�D����E���߶�CD���ӳ����ϣ�����QE������QDΪ���ĵ�����QDE������Ƿ�������ֵ�������ڣ������������ֵ���������ڣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
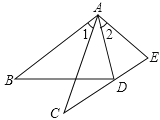
����Ŀ������ѧ���ϣ�����ʦ�ںڰ��ϻ�����ͼ��ʾ�ġ�ABD�͡�ACE���������Σ���д���ĸ���������AB=AC����AD=AE���ۡ�1=��2���ܡ�B=��C.��������ĸ�������ѡ��������Ϊ���裬��һ����Ϊ���ۣ����һ�������⣬������֤��.
���裺___________�����ۣ�_______.������д��ţ�
֤����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com