
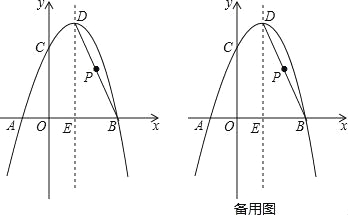
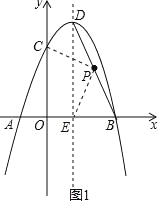
【题目】(2016广东省茂名市第25题)如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线的对称轴DE交x轴于点E,连接BD.
(1)求经过A,B,C三点的抛物线的函数表达式;
(2)点P是线段BD上一点,当PE=PC时,求点P的坐标;
(3)在(2)的条件下,过点P作PF⊥x轴于点F,G为抛物线上一动点,M为x轴上一动点,N为直线PF上一动点,当以F、M、G为顶点的四边形是正方形时,请求出点M的坐标.
【答案】(1)、y=﹣x2+2x+3;(2)、(2,2);(3)、(![]() ,0),(
,0),(![]() ,0),(
,0),(![]() ,0),(
,0),(![]() ,0).
,0).
【解析】
试题分析:(1)、利用待定系数法求出过A,B,C三点的抛物线的函数表达式;(2)、连接PC、PE,利用公式求出顶点D的坐标,利用待定系数法求出直线BD的解析式,设出点P的坐标为(x,﹣2x+6),利用勾股定理表示出PC2和PE2,根据题意列出方程,解方程求出x的值,计算求出点P的坐标;(3)、设点M的坐标为(a,0),表示出点G的坐标,根据正方形的性质列出方程,解方程即可.
试题解析:(1)、∵抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,
∴![]() , 解得,
, 解得,![]() , ∴经过A,B,C三点的抛物线的函数表达式为y=﹣x2+2x+3;
, ∴经过A,B,C三点的抛物线的函数表达式为y=﹣x2+2x+3;
(2)、如图1,连接PC、PE, x=﹣![]() =﹣
=﹣![]() =1, 当x=1时,y=4,
=1, 当x=1时,y=4,
∴点D的坐标为(1,4), 设直线BD的解析式为:y=mx+n,则![]() , 解得,
, 解得,![]() ,
,
∴直线BD的解析式为y=﹣2x+6, 设点P的坐标为(x,﹣2x+6),
则PC2=x2+(3+2x﹣6)2,PE2=(x﹣1)2+(﹣2x+6)2, ∵PC=PE,
∴x2+(3+2x﹣6)2=(x﹣1)2+(﹣2x+6)2, 解得,x=2, 则y=﹣2×2+6=2, ∴点P的坐标为(2,2);
(3)、设点M的坐标为(a,0),则点G的坐标为(a,﹣a2+2a+3),
∵以F、M、G为顶点的四边形是正方形, ∴FM=MG,即|2﹣a|=|﹣a2+2a+3|,
当2﹣a=﹣a2+2a+3时, 整理得,a2﹣3a﹣1=0, 解得,a=![]() ,
,
当2﹣a=﹣(﹣a2+2a+3)时, 整理得,a2﹣a﹣5=0, 解得,a=![]() ,
,
∴当以F、M、G为顶点的四边形是正方形时,点M的坐标为(![]() ,0),(
,0),(![]() ,0),(
,0),(![]() ,0),(
,0),(![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】某一型号飞机着陆后滑行的距离S(单位:米)关于滑行的时间t(单位:秒)之间的函数解析式是S=﹣1.5t2+60t,则该型号飞机着陆后滑行( )秒才能停下来.
A. 600 B. 300 C. 40 D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
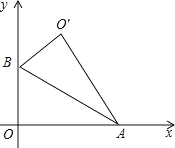
【题目】(2016宁夏第14题)如图,Rt△AOB中,∠AOB=90°,OA在x轴上,OB在y轴上,点A,B的坐标分别为(![]() ,0),(0,1),把Rt△AOB沿着AB对折得到Rt△AO′B,则点O′的坐标为 .
,0),(0,1),把Rt△AOB沿着AB对折得到Rt△AO′B,则点O′的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
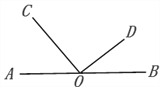
【题目】如图,O是直线AB上的一点,OC⊥OD,垂足为O.
(1)若∠BOD=32°,求∠AOC的度数;
(2)若∠AOC:∠BOD=2:1,直接写出∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC的平分线交CD于点E.
(1)若∠A=70°,求∠ABE的度数;
(2)若AB∥CD,且∠1=∠2,判断DF和BE是否平行,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随机从甲、乙两块试验田中各抽取100株麦苗测量高度,甲、乙两块试验田的平均数都是13,方差结果为:S甲2=36,S乙2=158,则小麦长势比较整齐的试验田是
查看答案和解析>>
科目:初中数学 来源: 题型:
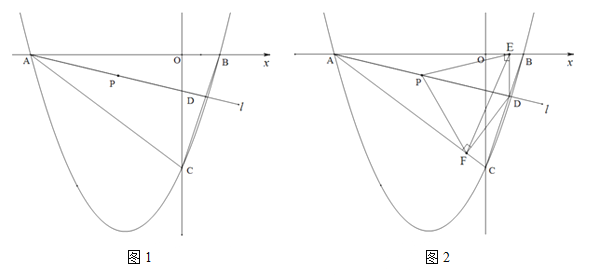
【题目】(2016四川省乐山市第26题)如图1,二次函数![]() 的图象与
的图象与![]() 轴分别交于A、B两点,与
轴分别交于A、B两点,与![]() 轴交于点C.若tan∠ABC=3,一元二次方程
轴交于点C.若tan∠ABC=3,一元二次方程![]() 的两根为-8、2.
的两根为-8、2.
(1)求二次函数的解析式;
(2)直线![]() 绕点A以AB为起始位置顺时针旋转到AC位置停止,
绕点A以AB为起始位置顺时针旋转到AC位置停止,![]() 与线段BC交于点D,P是AD的中点.
与线段BC交于点D,P是AD的中点.
①求点P的运动路程;
②如图2,过点D作DE垂直![]() 轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在
轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在![]() 运动过程中,∠EPF的大小是否改变?请说明理由;
运动过程中,∠EPF的大小是否改变?请说明理由;
(3)在(2)的条件下,连结![]() ,求△PEF周长的最小值.
,求△PEF周长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com