
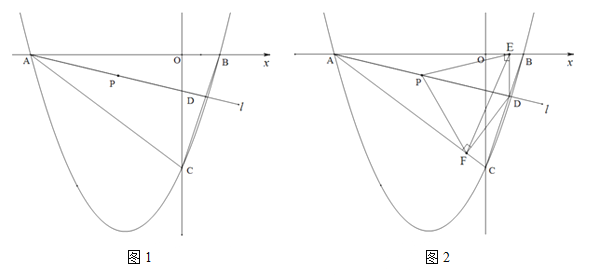
【题目】(2016四川省乐山市第26题)如图1,二次函数![]() 的图象与
的图象与![]() 轴分别交于A、B两点,与
轴分别交于A、B两点,与![]() 轴交于点C.若tan∠ABC=3,一元二次方程
轴交于点C.若tan∠ABC=3,一元二次方程![]() 的两根为-8、2.
的两根为-8、2.
(1)求二次函数的解析式;
(2)直线![]() 绕点A以AB为起始位置顺时针旋转到AC位置停止,
绕点A以AB为起始位置顺时针旋转到AC位置停止,![]() 与线段BC交于点D,P是AD的中点.
与线段BC交于点D,P是AD的中点.
①求点P的运动路程;
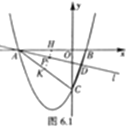
②如图2,过点D作DE垂直![]() 轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在
轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在![]() 运动过程中,∠EPF的大小是否改变?请说明理由;
运动过程中,∠EPF的大小是否改变?请说明理由;
(3)在(2)的条件下,连结![]() ,求△PEF周长的最小值.
,求△PEF周长的最小值.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②不变,理由见试题解析;(3)
;②不变,理由见试题解析;(3)![]() .
.
【解析】
试题分析:(1)由![]() 与
与![]() 轴分别交于A、B两点,且一元二次方程
轴分别交于A、B两点,且一元二次方程![]() 的两根为-8、2,可得点A、点B的坐标,即可得到OB的长,又由tan∠ABC=3,得到点C(0,-6),将 A、B、C的坐标代入二次函数中,即可得到二次函数解析式;
的两根为-8、2,可得点A、点B的坐标,即可得到OB的长,又由tan∠ABC=3,得到点C(0,-6),将 A、B、C的坐标代入二次函数中,即可得到二次函数解析式;
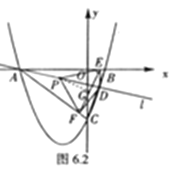
(2)①如图6.1,当l在AB位置时,P即为AB的中点H,当l运动到AC位置时,P即为AC的中点K,故P的运动路程为△ABC的中位线HK,在Rt△BOC中,由勾股定理得到BC的长,再由三角形中位线定理可得到HK的长,即P的运动路程;
②∠EPF的大小不会改变.由于,P为Rt△AED斜边AD的中点,故PE=![]() AD=PA,从而∠PAE=∠PEA=
AD=PA,从而∠PAE=∠PEA=![]() ∠EPD,同理有∠PAF=∠PFA=
∠EPD,同理有∠PAF=∠PFA=![]() ∠DPF,即可得到∠EPF=2∠EAF,故∠EPF的大小不会改变;
∠DPF,即可得到∠EPF=2∠EAF,故∠EPF的大小不会改变;
(3)设△PEF的周长为C,则![]() =PE+PF+EF=AD+EF,在等腰三角形PEF中,过P作PG⊥EF于点G,得到∠EPG=
=PE+PF+EF=AD+EF,在等腰三角形PEF中,过P作PG⊥EF于点G,得到∠EPG=![]() ∠EPF=∠BAC,由于tan∠BAC=
∠EPF=∠BAC,由于tan∠BAC=![]() ,故tan∠EPG=
,故tan∠EPG=![]() ,得到EG=
,得到EG=![]() PE,EF=
PE,EF=![]() PE=
PE=![]() AD,从而有
AD,从而有![]() =AD+EF=
=AD+EF=![]() AD=
AD=![]() AD,又当AD⊥BC时,AD最小,此时
AD,又当AD⊥BC时,AD最小,此时![]() 最小,由
最小,由![]() =30,得到AD=
=30,得到AD=![]() ,从而得到
,从而得到![]() 最小值.
最小值.
试题解析:(1)∵函数![]() 的图象与
的图象与![]() 轴分别交于A、B两点,且一元二次方程
轴分别交于A、B两点,且一元二次方程![]() 的两根为-8、2,∴A(-8,0)、B(2,0),即OB=2,又∵tan∠ABC=3,∴OC=6,即C(0,-6),将 A(-8,0)、B(2,0)代入
的两根为-8、2,∴A(-8,0)、B(2,0),即OB=2,又∵tan∠ABC=3,∴OC=6,即C(0,-6),将 A(-8,0)、B(2,0)代入![]() 中,解得:
中,解得:![]() ,
,![]() ,∴二次函数解析式为:
,∴二次函数解析式为:![]() ;
;
(2)①如图6.1,当l在AB位置时,P即为AB的中点H,当l运动到AC位置时,P即为AC的中点K,∴P的运动路程为△ABC的中位线HK,∴HK=![]() BC,在Rt△BOC中,OB=2,OC=6,∴BC=
BC,在Rt△BOC中,OB=2,OC=6,∴BC=![]() ,∴HK=
,∴HK=![]() ,即P的运动路程为
,即P的运动路程为![]() ;
;
②∠EPF的大小不会改变.理由如下:
∵DE⊥AB,∴在Rt△AED中,P为斜边AD的中点,∴PE=![]() AD=PA,∴∠PAE=∠PEA=
AD=PA,∴∠PAE=∠PEA=![]() ∠EPD,同理可得:∠PAF=∠PFA=
∠EPD,同理可得:∠PAF=∠PFA=![]() ∠DPF,∴∠EPF=∠EPD+∠FPD=2(∠PAE+∠PAF),即∠EPF=2∠EAF,又∵∠EAF大小不变,∴∠EPF的大小不会改变;
∠DPF,∴∠EPF=∠EPD+∠FPD=2(∠PAE+∠PAF),即∠EPF=2∠EAF,又∵∠EAF大小不变,∴∠EPF的大小不会改变;
(3)设△PEF的周长为C,则![]() =PE+PF+EF,∵PE=
=PE+PF+EF,∵PE=![]() AD,PF=
AD,PF=![]() AD,∴
AD,∴![]() =AD+EF,在等腰三角形PEF中,过P作PG⊥EF于点G,∴∠EPG=
=AD+EF,在等腰三角形PEF中,过P作PG⊥EF于点G,∴∠EPG=![]() ∠EPF=∠BAC,∵tan∠BAC=
∠EPF=∠BAC,∵tan∠BAC=![]() ,∴tan∠EPG=
,∴tan∠EPG=![]() ,∴EG=
,∴EG=![]() PE,EF=
PE,EF=![]() PE=
PE=![]() AD,∴
AD,∴![]() =AD+EF=
=AD+EF=![]() AD=
AD=![]() AD,又当AD⊥BC时,AD最小,此时
AD,又当AD⊥BC时,AD最小,此时![]() 最小,∵
最小,∵![]() =30,∴
=30,∴![]() BC·AD=30,∴AD=
BC·AD=30,∴AD=![]() ,∴
,∴![]() 最小值为:
最小值为:![]() AD=
AD=![]() .
.


科目:初中数学 来源: 题型:
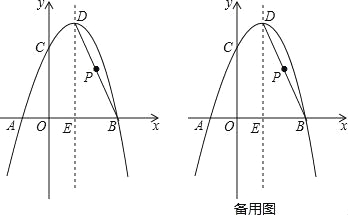
【题目】(2016广东省茂名市第25题)如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线的对称轴DE交x轴于点E,连接BD.
(1)求经过A,B,C三点的抛物线的函数表达式;
(2)点P是线段BD上一点,当PE=PC时,求点P的坐标;
(3)在(2)的条件下,过点P作PF⊥x轴于点F,G为抛物线上一动点,M为x轴上一动点,N为直线PF上一动点,当以F、M、G为顶点的四边形是正方形时,请求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、E在线段CD上,若∠C=∠D,则添加下列条件,不一定能使△ABC≌△EFD的是( )
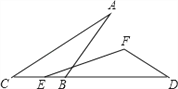
A. BC=FD,AC=ED B. ∠A=∠DEF,AC=ED
C. AC=ED,AB=EF D. ∠ABC=∠EFD,BC=FD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某公司有三个住宅区可看作一点,A,B,C各区分别住有职工30人、15人、10人,且这三个住宅区在一条大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
![]()
A. 点A B. 点B
C. A,B之间 D. B,C之间
查看答案和解析>>
科目:初中数学 来源: 题型:
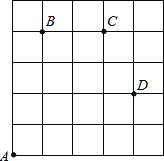
【题目】如图,一只甲虫在5×5的方格(每小格边长为1个单位长度)上沿着网格线运动,它从A处出发去看望B、C、D处的其它甲虫.规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从D到C记为:D→C(﹣1,+2),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中A→C可以记为( , ),B→C可以记为( , ).
(2)D→ 可以记为(﹣4,﹣2).
(3)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程长度为 ;
(4)若这只甲虫从A处去甲虫P处的行走路线依次为(+1,+3),(+3,﹣2),(﹣2,+1),请在图中标出P的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com