
【题目】如图,梯形ABCD中,AB∥CD,AB=14,AD= 4![]() , CD=7.直线l经过A,D两点,且sin∠DAB=
, CD=7.直线l经过A,D两点,且sin∠DAB=![]() . 动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于AB,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
. 动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于AB,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
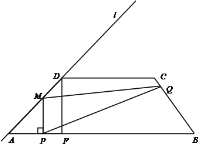
(1)求腰BC的长;
(2)当Q在BC上运动时,求S与t的函数关系式;
(3)在(2)的条件下,是否存在某一时刻t,使得△MPQ的面积S是梯形ABCD面积的![]() ?若存在,请求出t的值;若不存在,请说明理由;
?若存在,请求出t的值;若不存在,请说明理由;
(4)随着P,Q两点的运动,当点M在线段DC上运动时,设PM的延长线与直线l相交于点N,试探究:当t为何值时,△QMN为等腰三角形?
【答案】(1)5;(2)S=﹣5t2+14t(0<t≤1)(3)不存在,理由见解析;(4)t=![]() 或t=
或t=![]()
【解析】
试题(1)利用梯形性质确定点D的坐标,利用sin∠DAB=![]() 特殊三角函数值,得到△AOD为等腰直角三角形,求出梯形的高,然后利用勾股定理求出BC有长;
特殊三角函数值,得到△AOD为等腰直角三角形,求出梯形的高,然后利用勾股定理求出BC有长;
(2)当0<t≤1时,S=![]() ×2t×(14﹣5t)=﹣5t2+14t;
×2t×(14﹣5t)=﹣5t2+14t;
(3)在(2)的条件下,不存在某一时刻t,使得△MPQ的面积S是梯形ABCD面积的
(4)△QMN为等腰三角形的情形有两种,需要分类讨论,避免漏解.
试题解析:(1)5
(2)当0<t≤1时,S=![]() ×2t×(14﹣5t)=﹣5t2+14t
×2t×(14﹣5t)=﹣5t2+14t
(3)梯形ABCD的面积为42
﹣5t2+14t=![]()
![]() 42程无解,所以△MPQ的面积不能为梯形ABCD的
42程无解,所以△MPQ的面积不能为梯形ABCD的![]() 。
。
(4)△QMN为等腰三角形,有两种情形:
①如图4所示,点M在线段NM的右侧上
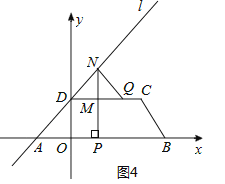 ,
,
MQ=CD-DM-CQ=7-(2t-4)-(5t-5)=16-7t,MN=DM=2t-4,
由MN=MQ,得16-7t=2t-4,解得t=![]() ;
;
②如图5所示,当Q在MN的左侧时,5t-5+(2t-4)-7=(2t-4)+4-4,
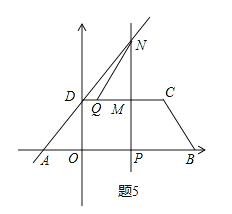
解得:t=![]() .
.
故当t=![]() 或t=
或t=![]() 时,△QMN为等腰三角形.
时,△QMN为等腰三角形.
考点: 一次函数综合题.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象分别与
的图象分别与![]() 轴和
轴和![]() 轴交于
轴交于![]() ,
,![]() 两点,且与正比例函数
两点,且与正比例函数![]() 的图象交于点
的图象交于点![]() .
.
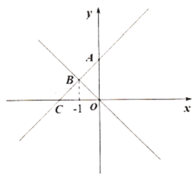
(1)求![]() 的值;
的值;
(2)求正比例函数的表达式;
(3)点![]() 是一次函数图象上的一点,且
是一次函数图象上的一点,且![]() 的面积是3,求点
的面积是3,求点![]() 的坐标;
的坐标;
(4)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 的值最小?若存在,求出点
的值最小?若存在,求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两商店出售同样的茶壶和茶杯,茶壶每只定价20元,茶杯每只定价5元,两家商店搞促销活动,甲店:买一只茶壶赠一只茶杯;乙店:按定价的9折优惠,某顾客需购买茶壶4只,茶杯若干只(不少于4只).
(1)设购买茶杯数为![]() (只),在甲店购买的付款为
(只),在甲店购买的付款为![]() (元),在乙店购买的付款数为
(元),在乙店购买的付款数为![]() (元),分别写出在两家商店购物的付款数与茶杯数
(元),分别写出在两家商店购物的付款数与茶杯数![]() 之间的关系式;
之间的关系式;
(2)当购买多少只茶杯时,两家商店的花费相同?
(3)当购买20只茶杯时,去哪家商店购物比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国家的宏观调控下,某市的商品房成交价由今年3月份的5000元/m2下降到5月份的4050元/m2.
(1)问4、5两月平均每月降价的百分率是多少?
(2)如果房价继续回落,按此降价的百分率,你预测到7月分该市的商品房成交均价是否会跌破3000元/m2?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2).
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,与射线
长为半径画弧,与射线![]() 相交于点
相交于点![]() ,连接
,连接![]() ,过
,过![]() 点作
点作![]() ,垂足为
,垂足为![]() .
.

(1)线段![]() 与图中现有的哪一条线段相等?你得出的结论是:
与图中现有的哪一条线段相等?你得出的结论是:![]() ;
;
(2)证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AC=BC,点D在△ABC外部,且∠ACB+∠ADB=180°,连接AB、CD.
(1)如图1,当∠ACB=90°时,则∠ADC=______°.
(2)如图2,当∠ACB=60°时,求证:DC平分∠ADB.

查看答案和解析>>
科目:初中数学 来源: 题型:
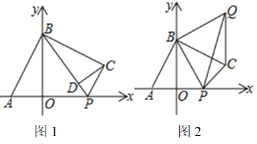
【题目】已知:如图,在平面直角坐标系中,A(a,0)、B(0,b),且|a+2|+(b+2a)2=0,点P为x轴上一动点,连接BP,在第一象限内作BC⊥AB且BC=AB
(1) 求点A、B的坐标
(2) 如图1,连接CP.当CP⊥BC时,作CD⊥BP于点D,求线段CD的长度
(3) 如图2,在第一象限内作BQ⊥BP且BQ=BP,连接PQ.设P(p,0),直接写出S△PCQ=_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC=10,sin∠BAC=![]() ,过点C作CD∥AB,点E在边AC上,AE=CD,联结AD,BE的延长线与射线CD、射线AD分别交于点F、G.设CD=x,△CEF的面积为y.
,过点C作CD∥AB,点E在边AC上,AE=CD,联结AD,BE的延长线与射线CD、射线AD分别交于点F、G.设CD=x,△CEF的面积为y.
(1)求证:∠ABE=∠CAD.
(2)如图,当点G在线段AD上时,求y关于x的函数解析式及定义域.
(3)若△DFG是直角三角形,求△CEF的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com