
【题目】在△ABC中,AB=AC=10,sin∠BAC=![]() ,过点C作CD∥AB,点E在边AC上,AE=CD,联结AD,BE的延长线与射线CD、射线AD分别交于点F、G.设CD=x,△CEF的面积为y.
,过点C作CD∥AB,点E在边AC上,AE=CD,联结AD,BE的延长线与射线CD、射线AD分别交于点F、G.设CD=x,△CEF的面积为y.
(1)求证:∠ABE=∠CAD.
(2)如图,当点G在线段AD上时,求y关于x的函数解析式及定义域.
(3)若△DFG是直角三角形,求△CEF的面积.

【答案】(1)见解析;(2)y=![]() (0<x≤5
(0<x≤5![]() -5);(3)若△DFG是直角三角形,则△CEF的面积为15或
-5);(3)若△DFG是直角三角形,则△CEF的面积为15或![]() .
.
【解析】
(1)由CD∥AB知∠BAC=∠ECD,结合AE=CD,AB=AC证△DAC≌△EBA即可得;
(2)作EH⊥AB,先表示出S△ABE=![]() ABEH=3x,再证∴△CEF∽△AEB,得
ABEH=3x,再证∴△CEF∽△AEB,得![]() =(
=(![]() )2,据此可得答案;
)2,据此可得答案;
(3)由∠DFG=∠EBA<∠ABC知∠DFG不可能为直角,从而分∠DGF=90°和∠GDF=90°两种情况分别求解.
(1)∵CD∥AB,
∴∠BAC=∠ECD,
又∵AE=CD,AB=AC,
∴△DAC≌△EBA(SAS),
∴∠ABE=∠CAD;
(2)过点E作EH⊥AB,垂足为H,
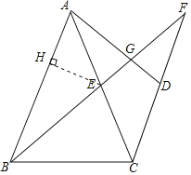
由题意知CE=AC-AE=10-x,EH=AEsin∠CAB=![]() x,
x,
∴AH=![]() x,
x,
则S△ABE=![]() ABEH=
ABEH=![]() ×10×
×10×![]() x=3x,
x=3x,
∵CF∥BA,
∴△CEF∽△AEB,
∴![]() =(
=(![]() )2,即
)2,即![]() =
=![]() ,
,
∴y=![]() (0<x≤5
(0<x≤5![]() -5);
-5);
(3)∵∠DFG=∠EBA<∠ABC,
∴∠DFG不可能为直角,
①当∠DGF=90°时,∠EGA=90°,
由∠GAE=∠GBA知△GAE∽△GBA,
∴tan∠GBA=![]() =
=![]() =
=![]() ,
,
在Rt△EHB中,tan∠GBA=![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得:x=0(舍)或x=5,
∴S△CEF=![]() =15;
=15;
②当∠GDF=90°时,∠BAG=90°,
由①知△GAE∽△GBA,
则∠AEB=∠GEA=90°,
∴BE=ABsin∠BAC=10×![]() =6,AE=
=6,AE=![]() =8,CE=AC-AE=2,
=8,CE=AC-AE=2,
由△CEF∽△AEB知![]() =
=![]() ,即
,即![]() =
=![]() ,
,
则EF=![]() ,
,
∴S△CEF=![]() ×EF×CE=
×EF×CE=![]() ×2×
×2×![]() =
=![]() ;
;
综上所述,若△DFG是直角三角形,则△CEF的面积为15或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AB∥CD,AB=14,AD= 4![]() , CD=7.直线l经过A,D两点,且sin∠DAB=
, CD=7.直线l经过A,D两点,且sin∠DAB=![]() . 动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于AB,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
. 动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于AB,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
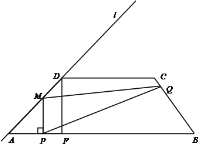
(1)求腰BC的长;
(2)当Q在BC上运动时,求S与t的函数关系式;
(3)在(2)的条件下,是否存在某一时刻t,使得△MPQ的面积S是梯形ABCD面积的![]() ?若存在,请求出t的值;若不存在,请说明理由;
?若存在,请求出t的值;若不存在,请说明理由;
(4)随着P,Q两点的运动,当点M在线段DC上运动时,设PM的延长线与直线l相交于点N,试探究:当t为何值时,△QMN为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地,两人之间的距离![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系如图所示,则下列说法正确的是( )
(分钟)之间的函数关系如图所示,则下列说法正确的是( )
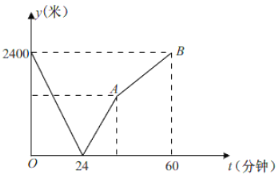
①当![]() 分钟时甲乙两人相遇;
分钟时甲乙两人相遇;
②甲的速度为40米/分钟;
③乙的速度为50米/分钟;
④乙到达目的地时,甲离目的地的距离为800米.
A.①②B.③④C.①②④D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
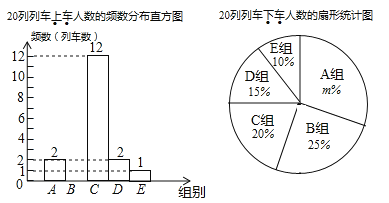
【题目】根据重庆轨道集团提供的日客运量统计,2019年2月21日重庆轨道交通首次日客运量突破300万乘次,其中近期开通的重庆轨道交通环线日客运量为21.5万乘次.据了解,某工作日上午7点至9点轨道环线四公里站有20列列车进出站,每列车进出站时,将上车和下车的人数记录下来,各得到20个数据,并将数据进行整理,绘制成了如下两幅不完整统计图.(数据分组为:![]() 组:
组:![]() ,
,![]() 组:
组:![]() ,
,![]() 组:
组:![]() ,
,![]() 组:
组:![]() ,
,![]() 组:
组:![]() )
)
I.上车人数在![]() 组的是:190,190,191,192,193,193,195,196,198,198,198,198;
组的是:190,190,191,192,193,193,195,196,198,198,198,198;
II.上车人数的平均数、中位数如下表:
平均数 | 中位数 | |
上车人数(人) | 194 | a |
根据以上信息,回答下列问题:
(1)请补全频数分布直方图;
(2)表中![]() ________,扇形统计图中
________,扇形统计图中![]() _________,扇形统计图中
_________,扇形统计图中![]() 组所在的圆心角度数为________度;
组所在的圆心角度数为________度;
(3)请利用平均数,估算一周内5个工作日的上午7点至9点重庆轨道环线四公里站的上车总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AB=9,cosA=![]() ,如果将△ABC绕着点C旋转至△A′B′C′的位置,使点B′落在∠ACB的角平分线上,A′B′与AC相交于点D,那么线段CD的长等于______.
,如果将△ABC绕着点C旋转至△A′B′C′的位置,使点B′落在∠ACB的角平分线上,A′B′与AC相交于点D,那么线段CD的长等于______.
查看答案和解析>>
科目:初中数学 来源: 题型:
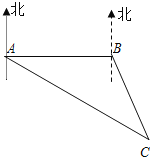
【题目】有一艘渔轮在海上C处作业时,发生故障,立即向搜救中心发出救援信号,此时搜救中心的两艘救助轮救助一号和救助二号分别位于海上A处和B处,B在A的正东方向,且相距100里,测得地点C在A的南偏东60,在B的南偏东30方向上,如图所示,若救助一号和救助二号的速度分别为40里/小时和30里/小时,问搜救中心应派那艘救助轮才能尽早赶到C处救援?(![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
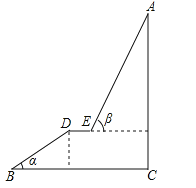
【题目】如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,∠BAD+∠BCD=180°, AC平分∠BAD,过点C作CE⊥AD,垂足为E, CD=4,AE=10,则四边形ABCD的周长是____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
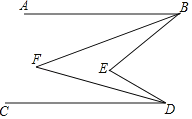
【题目】如图,已知AB∥CD.
(1)发现问题:若∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,则∠F与∠E的等量关系为 .
∠CDE,则∠F与∠E的等量关系为 .
(2)探究问题:若∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE.猜想:∠F与∠E的等量关系,并证明你的结论.
∠CDE.猜想:∠F与∠E的等量关系,并证明你的结论.
(3)归纳问题:若∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE.直接写出∠F与∠E的等量关系.
∠CDE.直接写出∠F与∠E的等量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com