【题目】学校与图书馆在同一条笔直道路上，甲从学校去图书馆，乙从图书馆回学校，甲、乙两人都匀速步行且同时出发，乙先到达目的地，两人之间的距离
（米）与时间
（分钟）之间的函数关系如图所示，则下列说法正确的是（ ）
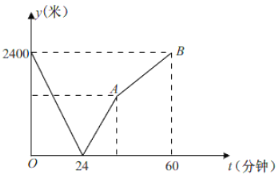
①当
分钟时甲乙两人相遇；
②甲的速度为40米/分钟；
③乙的速度为50米/分钟；
④乙到达目的地时，甲离目的地的距离为800米．
A.①②B.③④C.①②④D.①②③
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】甲乙两商店出售同样的茶壶和茶杯，茶壶每只定价20元，茶杯每只定价5元，两家商店搞促销活动，甲店：买一只茶壶赠一只茶杯；乙店：按定价的9折优惠，某顾客需购买茶壶4只，茶杯若干只（不少于4只）．
（1）设购买茶杯数为
（只），在甲店购买的付款为
（元），在乙店购买的付款数为
（元），分别写出在两家商店购物的付款数与茶杯数之间的关系式；
（2）当购买多少只茶杯时，两家商店的花费相同？
（3）当购买20只茶杯时，去哪家商店购物比较合算？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：在△ABC中，AC=BC，点D在△ABC外部，且∠ACB+∠ADB=180°，连接AB、CD.
(1)如图1，当∠ACB=90°时，则∠ADC=______°.
(2)如图2，当∠ACB=60°时，求证：DC平分∠ADB．
查看答案和解析>>
科目：初中数学 来源： 题型：
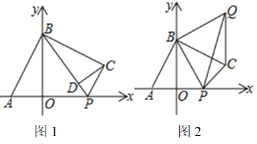
【题目】已知：如图，在平面直角坐标系中，A(a，0)、B(0，b)，且|a＋2|＋(b＋2a)2＝0，点P为x轴上一动点，连接BP，在第一象限内作BC⊥AB且BC＝AB
(1) 求点A、B的坐标
(2) 如图1，连接CP．当CP⊥BC时，作CD⊥BP于点D，求线段CD的长度
(3) 如图2，在第一象限内作BQ⊥BP且BQ＝BP，连接PQ．设P(p，0)，直接写出S△PCQ＝_____
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,某武警部队在一次地震抢险救灾行动中,探险队员在相距4米的水平地面A,B两处均探测出建筑物下方C处有生命迹象,已知在A处测得探测线与地面的夹角为30°,在B处测得探测线与地面的夹角为60°,求该生命迹象C所在位置的深度.(结果精确到0.1米,参考数据:
≈1.41,
≈1.73)
查看答案和解析>>
科目：初中数学 来源： 题型：
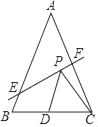
【题目】如图，△ABC的面积是12，AB=AC，BC=3，边AC的垂直平分线交AC于F，交AB于E．点D是BC的中点，点P是EF上的一个动点，则△PCD的周长最小值是( )
A.4B.8C.7D.9.5
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，AB=AC=10，sin∠BAC=
，过点C作CD∥AB，点E在边AC上，AE=CD，联结AD，BE的延长线与射线CD、射线AD分别交于点F、G．设CD=x，△CEF的面积为y．
（1）求证：∠ABE=∠CAD．
（2）如图，当点G在线段AD上时，求y关于x的函数解析式及定义域．
（3）若△DFG是直角三角形，求△CEF的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
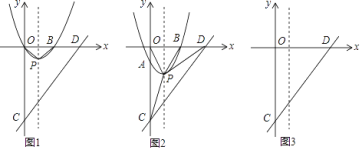
【题目】如图，平面直角坐标系中，抛物线y=x2﹣2x与x轴交于O、B两点，顶点为P，连接OP、BP，直线y=x﹣4与y轴交于点C，与x轴交于点D．
（1）写出点B坐标；判断△OBP的形状；
（2）将抛物线沿对称轴平移m个单位长度，平移的过程中交y轴于点A，分别连接CP、DP；
（i）若抛物线向下平移m个单位长度，当S△PCD= 
S△POC时，求平移后的抛物线的顶点坐标；
（ii）在平移过程中，试探究S△PCD和S△POD之间的数量关系，直接写出它们之间的数量关系及对应的m的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
