
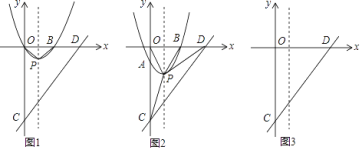
【题目】如图,平面直角坐标系中,抛物线y=x2﹣2x与x轴交于O、B两点,顶点为P,连接OP、BP,直线y=x﹣4与y轴交于点C,与x轴交于点D.
(1)写出点B坐标;判断△OBP的形状;
(2)将抛物线沿对称轴平移m个单位长度,平移的过程中交y轴于点A,分别连接CP、DP;
(i)若抛物线向下平移m个单位长度,当S△PCD= ![]() S△POC时,求平移后的抛物线的顶点坐标;
S△POC时,求平移后的抛物线的顶点坐标;
(ii)在平移过程中,试探究S△PCD和S△POD之间的数量关系,直接写出它们之间的数量关系及对应的m的取值范围.
【答案】(1)(2,0);等腰直角三角形;(2)(i)![]() 或
或![]() ;(ii)当m≥2时,S△POD﹣S△PCD=6;当﹣1≤m<2时,S△POD+S△PCD=6;当m<﹣1时,S△POD﹣S△PCD=6.
;(ii)当m≥2时,S△POD﹣S△PCD=6;当﹣1≤m<2时,S△POD+S△PCD=6;当m<﹣1时,S△POD﹣S△PCD=6.
【解析】
(1)根据自变量与函数值得对应关系,可得B点坐标,根据配方法,可得顶点坐标,根据勾股定理及勾股定理的逆定理,可得答案;
(2)根据自变量与函数值得对应关系,可得C,D,M点坐标,根据平移规律,可得P点坐标,根据平行于y轴的直线上两点间的距离较大的纵坐标减较小的纵坐标,可得PM的长,(i)根据面积的关系,可得关于m的方程,根据解方程,可得到顶点坐标;(ii)根据三角形的面积,可得答案.
(1)当y=0时,x2﹣2x=0,解得x=0(舍)或x=2,即B点坐标为(2,0),
∵抛物线y=x2﹣2x=(x﹣1)2﹣1,
∴P点坐标为(1,﹣1),由勾股定理,得
OP2=(2﹣1)2+12=2,
∴OP2+BP2=OB2 , OP=BP,
∴△OBP是等腰直角三角形,
(2)解:∵直线y=x﹣4与y轴交于点C,与x轴交于点D,
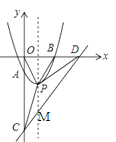
∴C(0,﹣4),D(4,0),当x=1时,y=﹣3,即M(1,﹣3),
抛物线向下平移m个单位长度,解析式为y=(x﹣1)2﹣(1+m),P(1,﹣1﹣m),
∴![]()
S△PCD=S△PMC+S△PMD= ![]() PM|xP﹣xC|=
PM|xP﹣xC|= ![]() |m﹣2|×4=2|m﹣2|,
|m﹣2|×4=2|m﹣2|,
(i)S△POC= ![]() AC|xP|=
AC|xP|= ![]() ×4×1=2,
×4×1=2,
∵S△PCD= ![]() S△POC,
S△POC,
∴S△PCD=2|m﹣2|=2![]() ,
,
解得m=2+ ![]() 或m=2﹣
或m=2﹣![]() ,
,
∴![]() 或
或![]() ;
;
(ii)![]()
①当m≥2时,S△PCD=2|m﹣2|=2m﹣4,S△POD=2|m+1|=2m+2,
∴S△POD﹣S△PCD=6
②当﹣1≤m<2时,S△PCD=2|m﹣2=4﹣2m,S△POD=2|m+1|=2m+2,
∴S△POD+S△PCD=6
③当m<﹣1时,S△PCD=2|m﹣2|=4﹣2m,S△POD=2|m+1|=2﹣2m,
∴S△POD﹣S△PCD=6,
综上所述:当m≥2时,S△POD﹣S△PCD=6;当﹣1≤m<2时,S△POD+S△PCD=6;当m<﹣1时,S△POD﹣S△PCD=6.


科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地,两人之间的距离![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系如图所示,则下列说法正确的是( )
(分钟)之间的函数关系如图所示,则下列说法正确的是( )
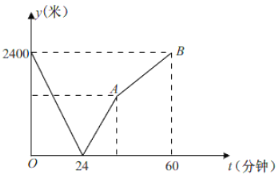
①当![]() 分钟时甲乙两人相遇;
分钟时甲乙两人相遇;
②甲的速度为40米/分钟;
③乙的速度为50米/分钟;
④乙到达目的地时,甲离目的地的距离为800米.
A.①②B.③④C.①②④D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
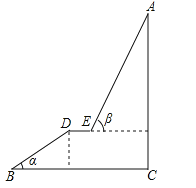
【题目】如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,∠BAD+∠BCD=180°, AC平分∠BAD,过点C作CE⊥AD,垂足为E, CD=4,AE=10,则四边形ABCD的周长是____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,那么△PBQ的面积S随出发时间t(s)如何变化?写出函数关系式及t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣3x2)(x3y)2;
(2)(x﹣5)(2x+1);
(3)(a﹣2)2﹣(a﹣1)(a+1);
(4)(3a﹣b+![]() )(3a﹣b﹣
)(3a﹣b﹣![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 为边
为边![]() 上的中线,点
上的中线,点![]() 在
在![]() 上,以点
上,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交
长为半径画弧,交![]() 的延长线于点
的延长线于点![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,连接
,连接![]() .
.
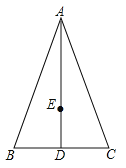
(1)依题意补全图形;
(2)求证:![]() ;
;
(3)若![]() 平分
平分![]() ,则
,则![]() 与
与![]() 满足的等量关系为 .
满足的等量关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
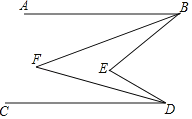
【题目】如图,已知AB∥CD.
(1)发现问题:若∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,则∠F与∠E的等量关系为 .
∠CDE,则∠F与∠E的等量关系为 .
(2)探究问题:若∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE.猜想:∠F与∠E的等量关系,并证明你的结论.
∠CDE.猜想:∠F与∠E的等量关系,并证明你的结论.
(3)归纳问题:若∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE.直接写出∠F与∠E的等量关系.
∠CDE.直接写出∠F与∠E的等量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).
ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).

A.AE=CFB.DE=BFC.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com