
【题目】如图,已知AB∥CD.
(1)发现问题:若∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,则∠F与∠E的等量关系为 .
∠CDE,则∠F与∠E的等量关系为 .
(2)探究问题:若∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE.猜想:∠F与∠E的等量关系,并证明你的结论.
∠CDE.猜想:∠F与∠E的等量关系,并证明你的结论.
(3)归纳问题:若∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE.直接写出∠F与∠E的等量关系.
∠CDE.直接写出∠F与∠E的等量关系.
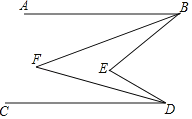
【答案】(1)∠BED=2∠BFD;(2)∠BED=3∠BFD,见解析;(3)∠BED=n∠BFD.
【解析】
(1)过点E,F分别作AB的平行线EG,FH,由平行线的传递性可得AB∥EG∥FH∥CD,根据平行线的性质得到∠ABF=∠BFH,∠CDF=∠DFH,从而得出∠BFD=∠CDF+∠ABF,同理可得出∠BED=∠ABE+∠CDE,最后可得出∠BED=2∠BFD;
(2)同(1)可知∠BFD=∠CDF+∠ABF,∠BED=∠ABE+∠CDE,再根据∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE即可得到结论;
∠CDE即可得到结论;
(3)同(1)(2)的方法即可得出∠F与∠E的等量关系.
解:(1)过点E、F分别作AB的平行线EG,FH,由平行线的传递性可得AB∥EG∥FH∥CD,
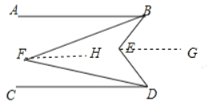
∵AB∥FH,
∴∠ABF=∠BFH,
∵FH∥CD,
∴∠CDF=∠DFH,
∴∠BFD=∠DFH+∠BFH=∠CDF+∠ABF;
同理可得∠BED=∠DEG+∠BEG=∠ABE+∠CDE,
∵∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,
∠CDE,
∴∠BFD=∠CDF+∠ABF=![]() (∠ABE+∠CDE)=
(∠ABE+∠CDE)=![]() ∠BED,
∠BED,
∴∠BED=2∠BFD.
故答案为:∠BED=2∠BFD;
(2)∠BED=3∠BFD.证明如下:
同(1)可得,
∠BFD=∠CDF+∠ABF,∠BED=∠ABE+∠CDE,
∵∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,
∠CDE,
∴∠BFD=∠CDF+∠ABF=![]() (∠ABE+∠CDE)=
(∠ABE+∠CDE)=![]() ∠BED,
∠BED,
∴∠BED=3∠BFD.
(3)同(1)(2)可得,
∠BFD=∠CDF+∠ABF,∠BED=∠ABE+∠CDE,
∵∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,
∠CDE,
∴∠BFD=∠CDF+∠ABF=![]() (∠ABE+∠CDE)=
(∠ABE+∠CDE)=![]() ∠BED,
∠BED,
∴∠BED=n∠BFD.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC=10,sin∠BAC=![]() ,过点C作CD∥AB,点E在边AC上,AE=CD,联结AD,BE的延长线与射线CD、射线AD分别交于点F、G.设CD=x,△CEF的面积为y.
,过点C作CD∥AB,点E在边AC上,AE=CD,联结AD,BE的延长线与射线CD、射线AD分别交于点F、G.设CD=x,△CEF的面积为y.
(1)求证:∠ABE=∠CAD.
(2)如图,当点G在线段AD上时,求y关于x的函数解析式及定义域.
(3)若△DFG是直角三角形,求△CEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
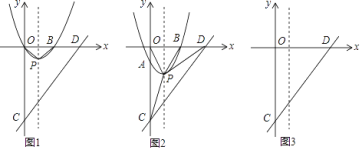
【题目】如图,平面直角坐标系中,抛物线y=x2﹣2x与x轴交于O、B两点,顶点为P,连接OP、BP,直线y=x﹣4与y轴交于点C,与x轴交于点D.
(1)写出点B坐标;判断△OBP的形状;
(2)将抛物线沿对称轴平移m个单位长度,平移的过程中交y轴于点A,分别连接CP、DP;
(i)若抛物线向下平移m个单位长度,当S△PCD= ![]() S△POC时,求平移后的抛物线的顶点坐标;
S△POC时,求平移后的抛物线的顶点坐标;
(ii)在平移过程中,试探究S△PCD和S△POD之间的数量关系,直接写出它们之间的数量关系及对应的m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,E是BC边的中点,BF∥AC,EF∥AB,EF=4 cm.
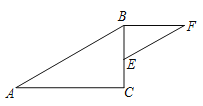
(1)求∠F的度数;
(2)求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“书香学校,书香班级”的建设号召,平顶山市某中学积极行动,学校图书角的新书、好书不断增加.下面是随机抽查该校若干名同学捐书情况统计图:
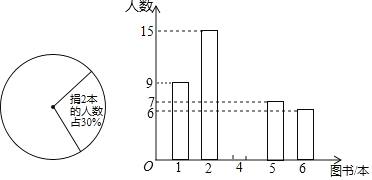
请根据下列统计图中的信息,解答下列问题:
(1)此次随机调查同学所捐图书数的中位数是 ,众数是 ;
(2)在扇形统计图中,捐2本书的人数所占的扇形圆心角是多少度?
(3)若该校有在校生1600名学生,估计该校捐4本书的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为3:4,∠OCD=90°,∠AOB=60°,若点B的坐标是(6,0),则点C的坐标是____.
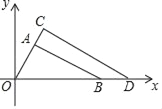
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一群女生住![]() 间宿舍,每间住4人,剩下18人无房住,每间住6人,有一间宿舍住不满,但有学生住.
间宿舍,每间住4人,剩下18人无房住,每间住6人,有一间宿舍住不满,但有学生住.
(1)用含![]() 的代数式表示女生人数.
的代数式表示女生人数.
(2)根据题意,列出关于![]() 的不等式组,并求不等式组的解集.
的不等式组,并求不等式组的解集.
(3)根据(2)的结论,问一共可能有多少间宿舍,多少名女生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将圆形转盘三等分,分别标上1、2、3三个数字,代表鸡、猴、鼠三种生肖邮票(每种邮票各两枚,鸡年邮票面值“0.80元”,其它邮票都是面值“1.20元”),转动转盘后,指针每落在某个数字所在扇形一次就表示获得该种邮票一枚.
(1)任意转动转盘一次,获得鸡年邮票的概率是 ;
(2)任意转动转盘两次,求获得的两枚邮票可以邮寄一封需2.4元邮资的信件的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com