
ΓΨΧβΡΩΓΩΈΣœλ”ΠΓΑ ιœψ―ß–ΘΘ§ ιœψΑύΦΕΓ±ΒΡΫ®…ηΚ≈’ΌΘ§ΤΫΕΞ…Ϋ –Ρ≥÷–―ßΜΐΦΪ––Ε·Θ§―ß–ΘΆΦ ιΫ«ΒΡ–¬ ιΓΔΚΟ ι≤ΜΕœ‘ωΦ”Θ°œ¬Οφ «ΥφΜζ≥ι≤ιΗΟ–Θ»τΗ…ΟϊΆ§―ßΨη ι«ιΩωΆ≥ΦΤΆΦΘΚ
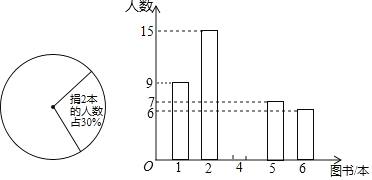
«κΗυΨίœ¬Ν–Ά≥ΦΤΆΦ÷–ΒΡ–≈œΔΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©¥Υ¥ΈΥφΜζΒς≤ιΆ§―ßΥυΨηΆΦ ι ΐΒΡ÷–ΈΜ ΐ «ΓΓ ΓΓΘ§÷Ύ ΐ «ΓΓ ΓΓΘΜ
Θ®2Θ©‘Ύ…»–ΈΆ≥ΦΤΆΦ÷–Θ§Ψη2±Ψ ιΒΡ»Υ ΐΥυ’ΦΒΡ…»–Έ‘≤–ΡΫ« «Εύ…ΌΕ»ΘΩ
Θ®3Θ©»τΗΟ–Θ”–‘Ύ–Θ…ζ1600Οϊ―ß…ζΘ§ΙάΦΤΗΟ–ΘΨη4±Ψ ιΒΡ―ß…ζ‘Φ”–Εύ…ΌΟϊΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©4±ΨΘΜ2±ΨΘΜΘ®2Θ©108ΓψΘΜΘ®3Θ©ΗΟ–ΘΨη4±Ψ ιΒΡ―ß…ζ‘Φ”–416ΟϊΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΨη2±ΨΒΡ―ß…ζ ΐΥυ’ΦΒΡΑΌΖ÷±»ΚΆ»Υ ΐΩ…“‘«σΒΟ±Ψ¥ΈΒς≤ιΒΡ―ß…ζ ΐΘ§¥”ΕχΩ…“‘ΒΟΒΫ÷–ΈΜ ΐΚΆ÷Ύ ΐΘΜ
Θ®2Θ©ΗυΨί…»–ΈΆ≥ΦΤΆΦ÷–ΒΡ ΐΨίΘ§άϊ”ΟΓΑ…»–Έ‘≤–ΡΫ«Ε» ΐ=360ΓψΓΝΥυ’ΦΑΌ±»άΐΓ±Φ¥Ω…ΒΟ≥ωΫαΙϊΘΜ
Θ®3Θ©ΗυΨί―υ±ΨΙάΦΤΉήΧεΒΡΖΫΖ®Θ§άϊ”Ο―ß…ζΉή»Υ ΐΓΝΨη4±Ψ ιΒΡ―ß…ζ»Υ ΐΥυ’ΦΒΡΑΌΖ÷±»Ω…ΒΟ≥ωΫαΙϊΘ°
ΫβΘΚΘ®1Θ©±Ψ¥ΈΒς≤ιΒΡ»Υ ΐΈΣΘΚ15Γ¬30%ΘΫ50Θ®»ΥΘ©Θ§
Ψη ι4±ΨΒΡ―ß…ζ»Υ ΐΈΣΘΚ50©¹9©¹15©¹7©¹6ΘΫ13Θ®»ΥΘ©Θ§
ΫΪΥυΨηΆΦ ι ΐΑ¥’’¥”–ΓΒΫ¥σΒΡΥ≥–ρ≈≈Ν–Θ§‘ρ¥Π‘ΎΒΎ25Θ§26ΈΜΒΡΨη ι ΐΕΦΈΣ4±ΨΘ§
Γύ¥Υ¥ΈΥφΜζΒς≤ιΆ§―ßΥυΨηΆΦ ι ΐΒΡ÷–ΈΜ ΐ «4±ΨΘΜ
ΗυΨίΆ≥ΦΤΆΦΩ…÷ΣΨη2±Ψ ιΒΡ»Υ ΐΉνΕύΘ§Γύ÷Ύ ΐ «2±ΨΘ§
Ι ¥πΑΗΈΣΘΚ4±ΨΘΜ2±ΨΘΜ
Θ®2Θ©ΗυΨίΧβ“βΒΟΘ§360ΓψΓΝ30%ΘΫ108ΓψΘ§
¥πΘΚΨη2±Ψ ιΒΡ»Υ ΐΥυ’ΦΒΡ…»–Έ‘≤–ΡΫ« «108ΓψΘΜ
Θ®3Θ©ΗυΨίΧβ“βΒΟΘ§1600ΓΝ![]() ΘΫ416Θ®ΟϊΘ©Θ§
ΘΫ416Θ®ΟϊΘ©Θ§
¥πΘΚΗΟ–ΘΨη4±Ψ ιΒΡ―ß…ζ‘Φ”–416ΟϊΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎRtΓςABC÷–Θ§ΓœACB=90ΓψΘ§AB=9Θ§cosA=![]() Θ§»γΙϊΫΪΓςABC»ΤΉ≈ΒψC–ΐΉΣ÷ΝΓςAΓδBΓδCΓδΒΡΈΜ÷ΟΘ§ ΙΒψBΓδ¬δ‘ΎΓœACBΒΡΫ«ΤΫΖ÷œΏ…œΘ§AΓδBΓδ”κACœύΫΜ”ΎΒψDΘ§Ρ«Ο¥œΏΕΈCDΒΡ≥ΛΒ»”Ύ______Θ°
Θ§»γΙϊΫΪΓςABC»ΤΉ≈ΒψC–ΐΉΣ÷ΝΓςAΓδBΓδCΓδΒΡΈΜ÷ΟΘ§ ΙΒψBΓδ¬δ‘ΎΓœACBΒΡΫ«ΤΫΖ÷œΏ…œΘ§AΓδBΓδ”κACœύΫΜ”ΎΒψDΘ§Ρ«Ο¥œΏΕΈCDΒΡ≥ΛΒ»”Ύ______Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§ΓœB=90ΓψΘ§AB=12Θ§BC=24Θ§Ε·ΒψP¥”ΒψAΩΣ Φ―Ί±ΏABœρ÷’ΒψB“‘ΟΩΟκ2ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»“ΤΕ·Θ§Ε·ΒψQ¥”ΒψBΩΣ Φ―Ί±ΏBC“‘ΟΩΟκ4ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»œρ÷’ΒψC“ΤΕ·Θ§»γΙϊΒψPΓΔQΖ÷±π¥”ΒψAΓΔBΆ§ ±≥ωΖΔΘ§Ρ«Ο¥ΓςPBQΒΡΟφΜΐSΥφ≥ωΖΔ ±ΦδtΘ®sΘ©»γΚΈ±δΜ·ΘΩ–¥≥ωΚ· ΐΙΊœΒ ΫΦΑtΒΡ»Γ÷ΒΖΕΈßΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() ΈΣ±Ώ
ΈΣ±Ώ![]() …œΒΡ÷–œΏΘ§Βψ
…œΒΡ÷–œΏΘ§Βψ![]() ‘Ύ
‘Ύ![]() …œΘ§“‘Βψ
…œΘ§“‘Βψ![]() ΈΣ‘≤–ΡΘ§
ΈΣ‘≤–ΡΘ§![]() ≥ΛΈΣΑκΨΕΜ≠ΜΓΘ§ΫΜ
≥ΛΈΣΑκΨΕΜ≠ΜΓΘ§ΫΜ![]() ΒΡ―”≥ΛœΏ”ΎΒψ
ΒΡ―”≥ΛœΏ”ΎΒψ![]() Θ§Βψ
Θ§Βψ![]() ‘Ύ
‘Ύ![]() …œΘ§«“
…œΘ§«“![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ°
Θ°
Θ®1Θ©“άΧβ“β≤Ι»ΪΆΦ–ΈΘΜ
Θ®2Θ©«σ÷ΛΘΚ![]() ΘΜ
ΘΜ
Θ®3Θ©»τ![]() ΤΫΖ÷
ΤΫΖ÷![]() Θ§‘ρ
Θ§‘ρ![]() ”κ
”κ![]() ¬ζΉψΒΡΒ»ΝΩΙΊœΒΈΣ Θ°
¬ζΉψΒΡΒ»ΝΩΙΊœΒΈΣ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
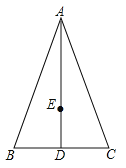
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΥΡ±Ώ–ΈABCD÷–Θ§AB=20Θ§BC=15Θ§CD=7Θ§AD=24Θ§ΓœB=90ΓψΘ°

Θ®1Θ©≈–ΕœΓœD «Ζώ «÷±Ϋ«Θ§≤ΔΥΒΟςάμ”…Θ°
Θ®2Θ©«σΥΡ±Ώ–ΈABCDΒΡΟφΜΐ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
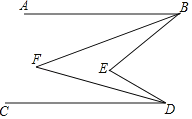
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣABΓΈCDΘ°
Θ®1Θ©ΖΔœ÷Έ ΧβΘΚ»τΓœABFΘΫ![]() ΓœABEΘ§ΓœCDFΘΫ
ΓœABEΘ§ΓœCDFΘΫ![]() ΓœCDEΘ§‘ρΓœF”κΓœEΒΡΒ»ΝΩΙΊœΒΈΣΓΓ ΓΓΘ°
ΓœCDEΘ§‘ρΓœF”κΓœEΒΡΒ»ΝΩΙΊœΒΈΣΓΓ ΓΓΘ°
Θ®2Θ©ΧΫΨΩΈ ΧβΘΚ»τΓœABFΘΫ![]() ΓœABEΘ§ΓœCDFΘΫ
ΓœABEΘ§ΓœCDFΘΫ![]() ΓœCDEΘ°≤¬œκΘΚΓœF”κΓœEΒΡΒ»ΝΩΙΊœΒΘ§≤Δ÷ΛΟςΡψΒΡΫα¬έΘ°
ΓœCDEΘ°≤¬œκΘΚΓœF”κΓœEΒΡΒ»ΝΩΙΊœΒΘ§≤Δ÷ΛΟςΡψΒΡΫα¬έΘ°
Θ®3Θ©ΙιΡ…Έ ΧβΘΚ»τΓœABFΘΫ![]() ΓœABEΘ§ΓœCDFΘΫ
ΓœABEΘ§ΓœCDFΘΫ![]() ΓœCDEΘ°÷±Ϋ”–¥≥ωΓœF”κΓœEΒΡΒ»ΝΩΙΊœΒΘ°
ΓœCDEΘ°÷±Ϋ”–¥≥ωΓœF”κΓœEΒΡΒ»ΝΩΙΊœΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ‘Ύ![]() ÷–Θ§
÷–Θ§![]() ΈΣ
ΈΣ![]() ΒΡ÷–ΒψΘ°
ΒΡ÷–ΒψΘ°
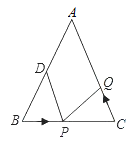
Θ®1Θ©»γΙϊΒψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œ“‘
…œ“‘![]() ΒΡΥΌΕ»”…Βψ
ΒΡΥΌΕ»”…Βψ![]() œρΒψ
œρΒψ![]() ‘ΥΕ·Θ§Ά§ ±Θ§Βψ
‘ΥΕ·Θ§Ά§ ±Θ§Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œ”…Βψ
…œ”…Βψ![]() œρΒψ
œρΒψ![]() ‘ΥΕ·Θ°
‘ΥΕ·Θ°
ΔΌ»τΒψ![]() ΒΡ‘ΥΕ·ΥΌΕ»”κΒψ
ΒΡ‘ΥΕ·ΥΌΕ»”κΒψ![]() ΒΡ‘ΥΕ·ΥΌΕ»œύΒ»Θ§
ΒΡ‘ΥΕ·ΥΌΕ»œύΒ»Θ§![]() ΚσΘ§
ΚσΘ§![]() ”κ
”κ![]() «Ζώ»ΪΒ»ΘΩ«κΥΒΟςάμ”…
«Ζώ»ΪΒ»ΘΩ«κΥΒΟςάμ”…
ΔΎ»τΒψ![]() ΒΡ‘ΥΕ·ΥΌΕ»”κΒψ
ΒΡ‘ΥΕ·ΥΌΕ»”κΒψ![]() ΒΡ‘ΥΕ·ΥΌΕ»≤ΜœύΒ»Θ§‘ρΒψ
ΒΡ‘ΥΕ·ΥΌΕ»≤ΜœύΒ»Θ§‘ρΒψ![]() ΒΡ‘ΥΕ·ΥΌΕ»ΈΣΕύ…Ό ±Θ§ΡήΙΜ Ι
ΒΡ‘ΥΕ·ΥΌΕ»ΈΣΕύ…Ό ±Θ§ΡήΙΜ Ι![]() ”κ
”κ![]() »ΪΒ»ΘΩ
»ΪΒ»ΘΩ
Θ®2Θ©»τΒψ![]() “‘ΒΎ
“‘ΒΎ![]() ΧβΔΎ÷–ΒΡ‘ΥΕ·ΥΌΕ»¥”Βψ
ΧβΔΎ÷–ΒΡ‘ΥΕ·ΥΌΕ»¥”Βψ![]() ≥ωΖΔΘ§Βψ
≥ωΖΔΘ§Βψ![]() “‘‘≠ά¥ΒΡ‘ΥΕ·ΥΌΕ»¥”Βψ
“‘‘≠ά¥ΒΡ‘ΥΕ·ΥΌΕ»¥”Βψ![]() Ά§ ±≥ωΖΔΘ§ΕΦΡφ ±’κ―Ί
Ά§ ±≥ωΖΔΘ§ΕΦΡφ ±’κ―Ί![]() »ΐ±Ώ‘ΥΕ·Θ§Ψ≠ΙΐΕύ…Ό ±ΦδΘ§Βψ
»ΐ±Ώ‘ΥΕ·Θ§Ψ≠ΙΐΕύ…Ό ±ΦδΘ§Βψ![]() ”κΒψ
”κΒψ![]() ΒΎ“Μ¥Έ‘Ύ
ΒΎ“Μ¥Έ‘Ύ![]() ΒΡΡΡΧθ±Ώ…œœύ”ωΘΩ
ΒΡΡΡΧθ±Ώ…œœύ”ωΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΚ÷ΣΙΊ”ΎxΒΡ“Μ‘ΣΕΰ¥ΈΖΫ≥Χx2+Θ®2k+3Θ©x+k2=0”–ΝΫΗω≤ΜœύΒ»ΒΡ Β ΐΗυx1Θ§x2Θ°
Θ®1Θ©«σkΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©»τ![]() =©¹1Θ§«σkΒΡ÷ΒΘ°
=©¹1Θ§«σkΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΨΊ–ΈOABC÷–Θ§ΒψOΈΣ‘≠ΒψΘ§ΒψAΒΡΉχ±ξΈΣΘ®0Θ§8Θ©Θ§ΒψCΒΡΉχ±ξΈΣΘ®6Θ§0Θ©Θ°≈ΉΈοœΏyΘΫ©¹![]() x2+bx+cΨ≠ΙΐΒψAΓΔCΘ§”κABΫΜ”ΎΒψDΘ°
x2+bx+cΨ≠ΙΐΒψAΓΔCΘ§”κABΫΜ”ΎΒψDΘ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΚ· ΐΫβΈω ΫΘΜ
Θ®2Θ©ΒψPΈΣœΏΕΈBC…œ“ΜΗωΕ·ΒψΘ®≤Μ”κΒψC÷ΊΚœΘ©Θ§ΒψQΈΣœΏΕΈAC…œ“ΜΗωΕ·ΒψΘ§AQΘΫCPΘ§Ν§Ϋ”PQΘ§…ηCPΘΫmΘ§ΓςCPQΒΡΟφΜΐΈΣSΘ°
ΔΌ«σSΙΊ”ΎmΒΡΚ· ΐ±μ¥ο ΫΘΜ
ΔΎΒ±SΉν¥σ ±Θ§‘Ύ≈ΉΈοœΏyΘΫ©¹![]() x2+bx+cΒΡΕ‘≥Τ÷αl…œΘ§»τ¥φ‘ΎΒψFΘ§ ΙΓςDFQΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§«κ÷±Ϋ”–¥≥ωΥυ”–ΖϊΚœΧθΦΰΒΡΒψFΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
x2+bx+cΒΡΕ‘≥Τ÷αl…œΘ§»τ¥φ‘ΎΒψFΘ§ ΙΓςDFQΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§«κ÷±Ϋ”–¥≥ωΥυ”–ΖϊΚœΧθΦΰΒΡΒψFΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
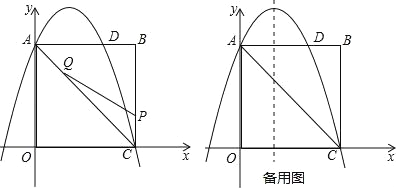
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com