
ЁОЬтФПЁПШчЭМЃЌвбжЊдк![]() жаЃЌ
жаЃЌ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЎ
ЕФжаЕуЃЎ
ЃЈ1ЃЉШчЙћЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯвд
ЩЯвд![]() ЕФЫйЖШгЩЕу
ЕФЫйЖШгЩЕу![]() ЯђЕу
ЯђЕу![]() дЫЖЏЃЌЭЌЪБЃЌЕу
дЫЖЏЃЌЭЌЪБЃЌЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯгЩЕу
ЩЯгЩЕу![]() ЯђЕу
ЯђЕу![]() дЫЖЏЃЎ
дЫЖЏЃЎ
ЂйШєЕу![]() ЕФдЫЖЏЫйЖШгыЕу
ЕФдЫЖЏЫйЖШгыЕу![]() ЕФдЫЖЏЫйЖШЯрЕШЃЌ
ЕФдЫЖЏЫйЖШЯрЕШЃЌ![]() КѓЃЌ
КѓЃЌ![]() гы
гы![]() ЪЧЗёШЋЕШЃПЧыЫЕУїРэгЩ
ЪЧЗёШЋЕШЃПЧыЫЕУїРэгЩ
ЂкШєЕу![]() ЕФдЫЖЏЫйЖШгыЕу
ЕФдЫЖЏЫйЖШгыЕу![]() ЕФдЫЖЏЫйЖШВЛЯрЕШЃЌдђЕу
ЕФдЫЖЏЫйЖШВЛЯрЕШЃЌдђЕу![]() ЕФдЫЖЏЫйЖШЮЊЖрЩйЪБЃЌФмЙЛЪЙ
ЕФдЫЖЏЫйЖШЮЊЖрЩйЪБЃЌФмЙЛЪЙ![]() гы
гы![]() ШЋЕШЃП
ШЋЕШЃП
ЃЈ2ЃЉШєЕу![]() вдЕк
вдЕк![]() ЬтЂкжаЕФдЫЖЏЫйЖШДгЕу
ЬтЂкжаЕФдЫЖЏЫйЖШДгЕу![]() ГіЗЂЃЌЕу
ГіЗЂЃЌЕу![]() вддРДЕФдЫЖЏЫйЖШДгЕу
вддРДЕФдЫЖЏЫйЖШДгЕу![]() ЭЌЪБГіЗЂЃЌЖМФцЪБеыби
ЭЌЪБГіЗЂЃЌЖМФцЪБеыби![]() Ш§БпдЫЖЏЃЌОЙ§ЖрЩйЪБМфЃЌЕу
Ш§БпдЫЖЏЃЌОЙ§ЖрЩйЪБМфЃЌЕу![]() гыЕу
гыЕу![]() ЕквЛДЮдк
ЕквЛДЮдк![]() ЕФФФЬѕБпЩЯЯргіЃП
ЕФФФЬѕБпЩЯЯргіЃП
ЁОД№АИЁПЃЈ1ЃЉЂйШЋЕШЃЌРэгЩМћНтЮіЃЛЂк3.75cm/sЃЛЃЈ2ЃЉ![]() sЃЌABБпЩЯ
sЃЌABБпЩЯ
ЁОНтЮіЁП
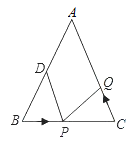
ЃЈ1ЃЉЂйЯШЧѓЕУBP=CQ=3ЃЌPC=BD=5ЃЌШЛКѓИљОнЕШБпЖдЕШНЧЧѓЕУЁЯB=ЁЯCЃЌдйИљОнSASМДПЩжЄУїЃЛ
ЂкЁїBPDЁеЁїCQPашТњзуBP=CPЃЌBD=CQЃЌЩшЕуQЕФЫйЖШЮЊvЃЌОЙ§tУыЗжБ№РћгУBP=CPЃЌBD=CQНЈСЂЗНГЬзщПЩЕУГіНсЙћЃЛ
ЃЈ3ЃЉЩшОЙ§xУыКѓЕуPгыЕуQЕквЛДЮЯргіЃЌСНЕуЯргіЪБЃЌТЗГЬВюЮЊ10+10ЃЌМДПЩЧѓГіЪБМфxЕФжЕЃЌШЗЖЈPЕФдЫЖЏТЗГЬЃЌИљОнвЛжмЕФГЄЖШЫуГіД№АИМДПЩЃЎ
ЃЈ1ЃЉЂйЁпt=1ЃЈУыЃЉЃЌ
ЁрBP=CQ=3ЃЈРхУзЃЉ
ЁпAB=10ЃЌDЮЊABжаЕуЃЌ
ЁрBD=5ЃЈРхУзЃЉ
гжЁпPC=BC-BP=8-3=5ЃЈРхУзЃЉ
ЁрPC=BD
ЁпAB=ACЃЌ
ЁрЁЯB=ЁЯCЃЌ
дкЁїBPDгыЁїCQPжаЃЌ
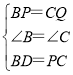 ЃЌ
ЃЌ
ЁрЁїBPDЁеЁїCQPЃЈSASЃЉЃЛ
ЂкЩшЕуQЕФЫйЖШЮЊvЃЌОЙ§tУыЁїBPDгыЁеЁїCQPЃЎ
вЊЪЙЁїBPDЁеЁїCQPЃЌБиаыТњзуBDЃНCQЃЌBPЃНPCЃЌ
МД![]() ЃЌ
ЃЌ
НтЕУ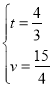 ЃЎ
ЃЎ
Д№ЃКЕуQЕФдЫЖЏЫйЖШЮЊ![]() РхУз/УыЪБЃЌФмЙЛЪЙЁїBPDЁеЁїCQPЃЎ
РхУз/УыЪБЃЌФмЙЛЪЙЁїBPDЁеЁїCQPЃЎ
ЃЈ2ЃЉЩшОЙ§xУыКѓЕуPгыЕуQЕквЛДЮЯргіЃЌгЩЬтвтЕУ
![]() xЃН3x+2ЁС10ЃЌ
xЃН3x+2ЁС10ЃЌ
НтЕУxЃН![]() ЃЌ
ЃЌ
ЕуPЙВдЫЖЏСЫ![]() ЁС3ЃН80РхУзЃЌ
ЁС3ЃН80РхУзЃЌ
80ЁТЃЈ8+10+10ЃЉЃН2![]() 24ЃЌМДдЫЖЏСЫ2ШІКѓдйдЫЖЏСЫ24РхУзЃЌдђДЫЪБдЫЖЏдкABЩЯЃЎ
24ЃЌМДдЫЖЏСЫ2ШІКѓдйдЫЖЏСЫ24РхУзЃЌдђДЫЪБдЫЖЏдкABЩЯЃЎ
Д№ЃКОЙ§![]() УыЃЌЕуPЃЌQдкЕквЛДЮдкБпABЩЯЯргіЃЎ
УыЃЌЕуPЃЌQдкЕквЛДЮдкБпABЩЯЯргіЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙДЙЩЖЈРэЪЧМИКЮбЇжаЕФУїжщЃЌГфТњзХїШСІЃЌЧЇАйФъРДЃЌШЫУЧЖдЫќЧїжЎШє№ЭЃЌЦфжагажјУћЕФЪ§бЇМвЃЌвВгавЕгрЪ§бЇАЎКУепЃЌЯђГЃДКдк1994ФъЙЙдьЗЂЯжСЫвЛИіаТЕФжЄЗЈЃКАбСНИіШЋЕШЕФжБНЧШ§НЧаЮШчЭМ1ЗХжУЃЌЦфШ§БпГЄЗжБ№ЮЊaЁЂbЁЂcЃЌЯдШЛЁЯDABЃНЁЯBЃН90ЁуЃЌACЁЭDEЃЎ
ЃЈ1ЃЉЧыгУaЁЂbЁЂcЗжБ№БэЪОГіЬнаЮABCDЁЂЫФБпаЮAECDЁЂЁїEBCЕФУцЛ§ЃЌдйЭЈЙ§ЬНОПетШ§ИіЭМаЮУцЛ§жЎМфЕФЙиЯЕЃЌжЄУїЃКЙДЙЩЖЈРэa2+b2ЃНc2ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЬњТЗЩЯAЁЂBСНЕуЃЈПДзїжБЯпЩЯЕФСНЕуЃЉЯрОр40ЧЇУзЃЌCЁЂDЮЊСНИіДхзЏЃЈПДзїСНИіЕуЃЉЃЌADЁЭABЃЌBCЁЭABЃЌДЙзуЗжБ№ЮЊAЁЂBЃЌADЃН24ЧЇУзЃЌBCЃН16ЧЇУзЃЌдкABЩЯгавЛИіЙЉгІеОPЃЌЧвPCЃНPDЃЌЧѓГіAPЕФОрРыЃЛ
ЃЈ3ЃЉНшжњЃЈ2ЃЉЕФЫМПМЙ§ГЬгыМИКЮФЃаЭЃЌжБНгаДГіДњЪ§ЪН![]() ЕФзюаЁжЕЮЊЁЁ ЁЁЃЎ
ЕФзюаЁжЕЮЊЁЁ ЁЁЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЁбOЕФАыОЖЮЊ10ЃЌдВаФOЕНЯвABЕФОрРыЮЊ5ЃЌдђЯвABЫљЖдЕФдВжмНЧЕФЖШЪ§ЪЧЃЈЁЁЁЁЃЉ
A. 30Ёу B. 60Ёу C. 30ЁуЛђ150Ёу D. 60ЁуЛђ120Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊЯьгІЁАЪщЯубЇаЃЃЌЪщЯуАрМЖЁБЕФНЈЩшКХейЃЌЦНЖЅЩНЪаФГжабЇЛ§МЋааЖЏЃЌбЇаЃЭМЪщНЧЕФаТЪщЁЂКУЪщВЛЖЯдіМгЃЎЯТУцЪЧЫцЛњГщВщИУаЃШєИЩУћЭЌбЇОшЪщЧщПіЭГМЦЭМЃК
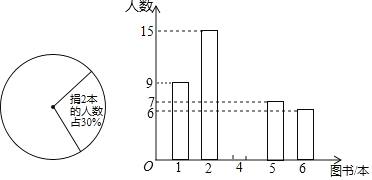
ЧыИљОнЯТСаЭГМЦЭМжаЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉДЫДЮЫцЛњЕїВщЭЌбЇЫљОшЭМЪщЪ§ЕФжаЮЛЪ§ЪЧЁЁ ЁЁЃЌжкЪ§ЪЧЁЁ ЁЁЃЛ
ЃЈ2ЃЉдкЩШаЮЭГМЦЭМжаЃЌОш2БОЪщЕФШЫЪ§ЫљеМЕФЩШаЮдВаФНЧЪЧЖрЩйЖШЃП
ЃЈ3ЃЉШєИУаЃгадкаЃЩњ1600УћбЇЩњЃЌЙРМЦИУаЃОш4БОЪщЕФбЇЩњдМгаЖрЩйУћЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЃКЙигкxЕФЖўДЮКЏЪ§![]() ЕФЭМЯѓгыxжсНЛгкЕуA(1ЃЌ0)КЭЕуBЃЌгыyжсНЛгкЕуC(0ЃЌ3)ЃЌХзЮяЯпЕФЖдГЦжсгыxжсНЛгкЕуD.
ЕФЭМЯѓгыxжсНЛгкЕуA(1ЃЌ0)КЭЕуBЃЌгыyжсНЛгкЕуC(0ЃЌ3)ЃЌХзЮяЯпЕФЖдГЦжсгыxжсНЛгкЕуD.
(1)ЧѓЖўДЮКЏЪ§ЕФБэДяЪНЃЛ
(2)дкyжсЩЯЪЧЗёДцдквЛЕуPЃЌЪЙЁїPBCЮЊЕШбќШ§НЧаЮ.ШєДцдкЃЌЧыЧѓГіЕуPЕФзјБъЃЛ
(3)гавЛИіЕуMДгЕуAГіЗЂЃЌвдУПУы1ИіЕЅЮЛЕФЫйЖШдкABЩЯЯђЕуBдЫЖЏЃЌСэвЛИіЕуNДгЕуDгыЕуMЭЌЪБГіЗЂЃЌвдУПУы2ИіЕЅЮЛЕФЫйЖШдкХзЮяЯпЕФЖдГЦжсЩЯдЫЖЏЃЌЕБЕуMЕН ДяЕуBЪБЃЌЕуMЁЂNЭЌЪБЭЃжЙдЫЖЏЃЌЮЪЕуMЁЂNдЫЖЏЕНКЮДІЪБЃЌЁїMNBУцЛ§зюДѓЃЌЪдЧѓГізюДѓУцЛ§.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
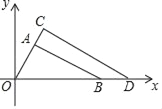
ЁОЬтФПЁПШчЭМЃЌЁїOABгыЁїOCDЪЧвдЕуOЮЊЮЛЫЦжааФЕФЮЛЫЦЭМаЮЃЌЯрЫЦБШЮЊ3ЃК4ЃЌЁЯOCD=90ЁуЃЌЁЯAOB=60ЁуЃЌШєЕуBЕФзјБъЪЧЃЈ6ЃЌ0ЃЉЃЌдђЕуCЕФзјБъЪЧ____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЯњЪлЩЬзМБИдкФЯГфВЩЙКвЛХњЫПГёЃЌОЕїВщЃЌгУ10000дЊВЩЙКAаЭЫПГёЕФМўЪ§гыгУ8000дЊВЩЙКBаЭЫПГёЕФМўЪ§ЯрЕШЃЌвЛМўAаЭЫПГёНјМлБШвЛМўBаЭЫПГёНјМлЖр100дЊЃЎ
ЃЈ1ЃЉЧѓвЛМўAаЭЁЂBаЭЫПГёЕФНјМлЗжБ№ЮЊЖрЩйдЊЃП
ЃЈ2ЃЉШєЯњЪлЩЬЙКНјAаЭЁЂBаЭЫПГёЙВ50МўЃЌЦфжаAаЭЕФМўЪ§ВЛДѓгкBаЭЕФМўЪ§ЃЌЧвВЛЩйгк16МўЃЌЩшЙКНјAаЭЫПГёmМўЃЎ
ЂйЧѓmЕФШЁжЕЗЖЮЇЃЎ
ЂквбжЊAаЭЕФЪлМлЪЧ800дЊ/МўЃЌЯњЪлГЩБОЮЊ2nдЊ/МўЃЛBаЭЕФЪлМлЮЊ600дЊ/МўЃЌЯњЪлГЩБОЮЊnдЊ/МўЃЎШчЙћ50ЁмnЁм150ЃЌЧѓЯњЪлетХњЫПГёЕФзюДѓРћШѓwЃЈдЊЃЉгыnЃЈдЊЃЉЕФКЏЪ§ЙиЯЕЪНЃЈУПМўЯњЪлРћШѓ=ЪлМлЉНјМлЉЯњЪлГЩБОЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
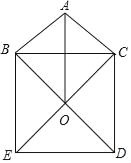
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=4ЃЌAC=3ЃЌвдBCЮЊБпдкШ§НЧаЮЭтзїе§ЗНаЮBCDEЃЌСЌНгBDЃЌCEНЛгкЕуOЃЌдђЯпЖЮAOЕФзюДѓжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌABЃН8cmЃЌBC=16cmЃЌЖЏЕуPДгЕуAПЊЪМбиABдЫЖЏЃЌЫйЖШЮЊ2cm/sЃЛЖЏЕуQДгЕуBПЊЪМбиBCдЫЖЏЃЌЫйЖШЮЊ4cm/sЃЎЩшPЁЂQСНЕуЭЌЪБдЫЖЏЃЌдЫЖЏЪБМфЮЊtsЃЈ0<t<4ЃЉ,ЕБЁїQBPгыЁїABCЯрЫЦЪБЃЌЧѓtЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com