
【题目】勾股定理是几何学中的明珠,充满着魅力,千百年来,人们对它趋之若鹜,其中有著名的数学家,也有业余数学爱好者,向常春在1994年构造发现了一个新的证法:把两个全等的直角三角形如图1放置,其三边长分别为a、b、c,显然∠DAB=∠B=90°,AC⊥DE.
(1)请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再通过探究这三个图形面积之间的关系,证明:勾股定理a2+b2=c2;
(2)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=24千米,BC=16千米,在AB上有一个供应站P,且PC=PD,求出AP的距离;
(3)借助(2)的思考过程与几何模型,直接写出代数式![]() 的最小值为 .
的最小值为 .

【答案】(1)见解析;(2)16千米;(3)20 .
【解析】
(1)表示出三个图形的面积进行加减计算可证a2+b2=c2
(2)以(1)中关于直角三角形的结论和K型模型建立方程关系,解方程可得AP的值
(3)将条件中的数表示为直角三角形的直角边,画对应图形,作轴对称图形,在三点共线时有最小值.
解:(1)梯形ABCD的面积![]()
四边形AECD的面积![]()
△EBC的面积![]()
∵梯形ABCD的面积=四边形AECD的面积+△EBC的面积
∴![]()
∴a2+b2=c2
(2)如图,当DP=PC时
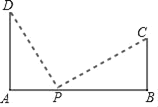
设AP=a,BP=40﹣a
∵DP2=CP2
∴AP2+AD2=BP2+CB2
∴a2+242=(40﹣a)2+162
解得 a=16
∴AP=16千米
(3)如图,![]()
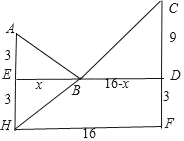
∴AB+BC的最小值即为H、B、C三点共线时
HC=![]() =20
=20
∴ 的最小值为20
的最小值为20
故答案为:20


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时![]() 张用A方法,其余用B方法。
张用A方法,其余用B方法。
(1)用![]() 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的轨道上有两个点甲与乙,开始时甲在A处,乙在C处,它们沿着正方形轨道顺时针同时出发,甲的速度为每秒1 cm,乙的速度为每秒5 cm,已知正方形轨道ABCD的边长为2 cm,则乙在第2 020次追上甲时的位置在( )
A.AB上B.BC上
C.CD上D.AD上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校要从甲乙两名射击运动员中挑选一人参加全市比赛,在选拔赛中,每人进行了5次射击,甲的成绩(环)为:9.7,10,9.6,9.8,9.9;乙的成绩的平均数为9.8,方差为0.032;
(1)甲的射击成绩的平均数和方差分别是多少?
(2)据估计,如果成绩的平均数达到9.8环就可能夺得金牌,为了夺得金牌,应选谁参加比赛?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的边长为4,对角线相交于点P,顶点A、C分别在x轴、y轴的正半轴上,抛物线L经过0、P、A三点,点E是正方形内的抛物线上的动点.
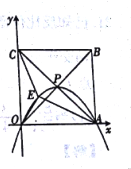
(1)点P的坐标为______
(2)求抛物线L的解析式.
(3)求△OAE与△OCE的面积之和的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() ,
,![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() ,
,![]() ,
,![]() ,
,![]() 两点之间的距离表示为
两点之间的距离表示为![]() ,在数轴上
,在数轴上![]() ,
,![]() 两点之间的距离
两点之间的距离![]() .已知数轴上
.已知数轴上![]() ,
,![]() 两点表示数
两点表示数![]() ,
,![]() 满足
满足![]() ,点
,点![]() 为数轴上一动点,其对应的数为
为数轴上一动点,其对应的数为![]() .
.
![]()
(1)![]() ,
,![]() 两点之间的距离是.
两点之间的距离是.
(2)![]() 与
与![]() 之间的距离表示为.
之间的距离表示为.
(3)数轴上是否存在点![]() ,使点
,使点![]() 到点
到点![]() ,点
,点![]() 的距离之和为
的距离之和为![]() ?若存在,请求出
?若存在,请求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(4)现在点![]() ,点
,点![]() 分别以
分别以![]() 单位/秒和
单位/秒和![]() 单位/秒的速度同时向右运动,当点
单位/秒的速度同时向右运动,当点![]() 与点
与点![]() 之间的距离为
之间的距离为![]() 个单位长度时,求点
个单位长度时,求点![]() 所对应的数是多少?
所对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意, 补全解题过程:
如图,∠AOB=90°,OE平分∠AOC,OF平分∠BOC. 求∠EOF的度数.
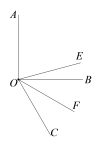
解:因为OE平分∠AOC,OF平分∠BOC
所以∠EOC =![]() ∠AOC,∠FOC =
∠AOC,∠FOC =![]() ________.
________.
所以∠EOF =∠EOC-________
=![]() (∠AOC-_______)
(∠AOC-_______)
=![]() ________
________
=_________°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】夏师傅是一名徒步运动的爱好者,他用手机软件记录了某个月(30天)每天徒步的步数(单位:万步),将记录结果绘制成了如图所示的统计图.在这组徒步数据中,众数和中位数分别是( )

A. 1.2,1.3 B. 1.4,1.3 C. 1.4,1.35 D. 1.3,1.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com