
【题目】如图,正方形OABC的边长为4,对角线相交于点P,顶点A、C分别在x轴、y轴的正半轴上,抛物线L经过0、P、A三点,点E是正方形内的抛物线上的动点.
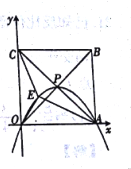
(1)点P的坐标为______
(2)求抛物线L的解析式.
(3)求△OAE与△OCE的面积之和的最大值.
【答案】(1)(2,2);(2)![]() ;(3)9.
;(3)9.
【解析】试题分析:(1)根据正方形的边长结合正方形的性质即可得出点![]() 三点的坐标;
三点的坐标;
(2)设抛物线L的解析式为![]() 结合点
结合点![]() 的坐标利用待定系数法即可求出抛物线的解析式;
的坐标利用待定系数法即可求出抛物线的解析式;
(3)由点![]() 为正方形内的抛物线上的动点,设出点
为正方形内的抛物线上的动点,设出点![]() 的坐标,结合三角形的面积公式找出
的坐标,结合三角形的面积公式找出![]() 关于
关于![]() 的函数解析式,根据二次函数的性质即可得出结论.
的函数解析式,根据二次函数的性质即可得出结论.
试题解析:(1)∵OABC为正方形,且边长为4,对角线相交于点P,
∴点O的坐标为(0,0),点B的坐标为(4,4),点P为OB的中点,
∴点P的坐标为(2,2).
故答案为:(2,2).
(2)设抛物线L的解析式为![]()
∵抛物线L经过O、P、A三点,
∴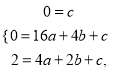 解得:
解得: 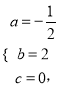
∴抛物线L的解析式为![]()
(3)∵点E是正方形内的抛物线上的动点,
∴设点E的坐标为![]()
∴![]()
∴当m=3时,△OAE与△OCE面积之和最大,最大值为9.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在数轴上有 A 、B 、C 、D 四个点,分别对应的数为 a ,b , c , d ,且满足 a ,b 是方程| x7|1的两个解(a b),且(c 12)2 与| d 16 |互为相反数.

(1)填空: a 、b 、 c 、 d ;
(2)若线段 AB 以 3 个单位/ 秒的速度向右匀速运动,同时线段CD 以 1 单位长度/ 秒向左匀速运动,并设运动时间为t 秒,A 、B 两点都运动在线段CD 上(不与C , D 两个端点重合),若BD2AC ,求t 的值;
(3)在(2)的条件下,线段 AB ,线段CD 继续运动,当点 B 运动到点 D 的右侧时,问是否存在时间t ,使 BC3AD ?若存在,求t 的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
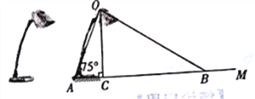
【题目】图为放置在水平桌面上的台灯的平面示意图,可伸缩式灯臂AO长为40 cm,与水平面所形成的夹角∠OAM恒为75°(不受灯臂伸缩的影响).由光源0射出的光线沿灯罩形成光线OC,OB,与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°.
(1)求该台灯照亮桌面的宽度BC.(不考虑其他因素,结果精确到1 cm,参考数据:sin75°≈0.97,cos75°≈0.26, ![]() ≈1.73)
≈1.73)
(2)若灯臂最多可伸长至60 cm,不调整灯罩的角度,能否让台灯照亮桌面85 cm的宽度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对数轴上的点![]() 进行如下操作:先把点
进行如下操作:先把点![]() 表示的数乘以3,再把所得数对应的点向左平移1个单位,得到点
表示的数乘以3,再把所得数对应的点向左平移1个单位,得到点![]() 的对应点
的对应点![]() .比如,点
.比如,点![]() 表示3,3乘以3得9,表示9的点向左平移1个单位为8,因此点
表示3,3乘以3得9,表示9的点向左平移1个单位为8,因此点![]() 的对应点
的对应点![]() 表示的数为8.
表示的数为8.
⑴点![]() ,
,![]() 在数轴上,对线段
在数轴上,对线段![]() 上的每个点进行上述操作后得到线段
上的每个点进行上述操作后得到线段![]() ,其中点
,其中点![]() ,
,![]() 的对应点分别为
的对应点分别为![]() ,
,![]() .如图,若点
.如图,若点![]() 表示的数是1,则点
表示的数是1,则点![]() 表示的数是__________;若点
表示的数是__________;若点![]() 表示的数是
表示的数是![]() ,则点
,则点![]() 表示的数是__________.
表示的数是__________.
⑵若数轴上的点![]() 经过上述操作后,位置不变,则点
经过上述操作后,位置不变,则点![]() 表示的数是__________.
表示的数是__________.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是几何学中的明珠,充满着魅力,千百年来,人们对它趋之若鹜,其中有著名的数学家,也有业余数学爱好者,向常春在1994年构造发现了一个新的证法:把两个全等的直角三角形如图1放置,其三边长分别为a、b、c,显然∠DAB=∠B=90°,AC⊥DE.
(1)请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再通过探究这三个图形面积之间的关系,证明:勾股定理a2+b2=c2;
(2)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=24千米,BC=16千米,在AB上有一个供应站P,且PC=PD,求出AP的距离;
(3)借助(2)的思考过程与几何模型,直接写出代数式![]() 的最小值为 .
的最小值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )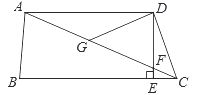
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小张某天下午的运营是在一条东西走向的大道上。如果规定向东为正,他这天下午的行程记录如下:(单位:千米)
+15,-3,+14,-11,+10,-18,+14
(1)将最后一名乘客送到目的地时,小张离下午出车点的距离是多少?
(2)离开下午出发点最远时是多少千米?
(3)若汽车的耗油量为0.06升/千米,油价为4.5元/升,这天下午共需支付多少油钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:菱形ABCD中,∠B=60°,将含60°角的直角三角板的60°角的顶点放到菱形ABCD的顶点A处,两边分别与菱形的边BC,CD交于点F,E.
(1)(如图1)求证:AE=AF;
(2)连结EF,交AC于点H(如图2),试探究AB,AF,AH之间的关系;
(3)若AB=6,EF=2![]() ,且CE<DE,求FH的长.
,且CE<DE,求FH的长.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com