
【题目】如图,在数轴上有 A 、B 、C 、D 四个点,分别对应的数为 a ,b , c , d ,且满足 a ,b 是方程| x7|1的两个解(a b),且(c 12)2 与| d 16 |互为相反数.

(1)填空: a 、b 、 c 、 d ;
(2)若线段 AB 以 3 个单位/ 秒的速度向右匀速运动,同时线段CD 以 1 单位长度/ 秒向左匀速运动,并设运动时间为t 秒,A 、B 两点都运动在线段CD 上(不与C , D 两个端点重合),若BD2AC ,求t 的值;
(3)在(2)的条件下,线段 AB ,线段CD 继续运动,当点 B 运动到点 D 的右侧时,问是否存在时间t ,使 BC3AD ?若存在,求t 的值;若不存在,说明理由.
【答案】(1)a 8 , b 6,c 12 , d 16;(2)![]() ;(3)t
;(3)t ![]() 或t
或t ![]() 时, BC 3AD
时, BC 3AD
【解析】
(1)根据绝对值的含义![]() (
(![]() 为正数) 及平方和绝对值的非负性
为正数) 及平方和绝对值的非负性![]() 即可求解;(2)AB 、CD 运动时, 点 A 对应的数为: 8 3t , 点 B 对应的数为: 6 3t , 点C 对应的数为:12 t , 点 D 对应的数为: 16 t ,根据题意列出关于t的等式求解即可;(3)根据题意求出t的取值范围,用含t的式子表示出BC和AD,再根据BC3AD即可求出t值.
即可求解;(2)AB 、CD 运动时, 点 A 对应的数为: 8 3t , 点 B 对应的数为: 6 3t , 点C 对应的数为:12 t , 点 D 对应的数为: 16 t ,根据题意列出关于t的等式求解即可;(3)根据题意求出t的取值范围,用含t的式子表示出BC和AD,再根据BC3AD即可求出t值.
(1)| x 7 | 1,
x 8 或6
a 8 , b 6,
(c 12)2 | d 16 | 0 ,
c 12 , d 16
(2) AB 、CD 运动时, 点 A 对应的数为: 8 3t , 点 B 对应的数为: 6 3t , 点C 对应的数为:12 t , 点 D 对应的数为: 16 t ,
BD |16 t (6 3t) || 22 4t |
AC |12 t (8 3t) || 20 4t |
BD 2 AC ,
22 4t 2(20 4t)
解得: ![]() 或
或![]()
当![]() 时,此时点 B 对应的数为
时,此时点 B 对应的数为![]() ,点C 对应的数为
,点C 对应的数为![]() ,此时不满足题意,
,此时不满足题意,
故![]()
(3)当点 B 运动到点 D 的右侧时, 此时
![]() ,
,
BC |12 t (6 3t ) ||18 4t | ,
AD |16 t (8 3t) || 24 4t | ,
BC 3AD ,
|18 4t | 3 | 24 4t | ,
解得: t ![]() 或t
或t ![]()
经验证,t ![]() 或t
或t ![]() , BC 3AD
, BC 3AD


科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点![]() 表示
表示![]() ,点
,点![]() 表示
表示![]() ,点
,点![]() 表示
表示![]() .动点
.动点![]() 从点
从点![]() 出发,沿数轴正方向以每秒
出发,沿数轴正方向以每秒![]() 个单位的速度匀速运动;同时,动点
个单位的速度匀速运动;同时,动点![]() 从点
从点![]() 出发,沿数轴负方向以每秒
出发,沿数轴负方向以每秒![]() 个单位的速度匀速运动.设运动时间为
个单位的速度匀速运动.设运动时间为![]() 秒.
秒.
(1)当![]() 为何值时,
为何值时,![]() 、
、![]() 两点相遇?相遇点
两点相遇?相遇点![]() 所对应的数是多少?
所对应的数是多少?
(2)在点![]() 出发后到达点
出发后到达点![]() 之前,求
之前,求![]() 为何值时,点
为何值时,点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到点
到点![]() 的距离相等;
的距离相等;
(3)在点![]() 向右运动的过程中,
向右运动的过程中,![]() 是
是![]() 的中点,在点
的中点,在点![]() 到达点
到达点![]() 之前,求
之前,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.

(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() 的图象与一次函数y=kx+m的图象相交于点A(2,1).
的图象与一次函数y=kx+m的图象相交于点A(2,1).
(1)分别求出这两个函数的解析式;
(2)当x取什么范围时,反比例函数值大于0;
(3)若一次函数与反比例函数另一交点为B,且纵坐标为﹣4,当x取什么范围时,反比例函数值大于一次函数的值;
(4)试判断点P(﹣1,5)关于x轴的对称点P′是否在一次函数y=kx+m的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古代有着辉煌的数学成就,《周牌算经》、《九章算术》、《海岛算经》、《孙子算经》等是我国古代数学的重要文献.
(1)小聪想从这4部数学名著中随机选择1部阅读,求他选中《九章算术》的概率;
(2)小聪拟从这4部数学名著中选择2部作为假课外拓展学习内容,用列表或树状图求选中的名著恰好是《九章算术》和《周牌算经》的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的轨道上有两个点甲与乙,开始时甲在A处,乙在C处,它们沿着正方形轨道顺时针同时出发,甲的速度为每秒1 cm,乙的速度为每秒5 cm,已知正方形轨道ABCD的边长为2 cm,则乙在第2 020次追上甲时的位置在( )
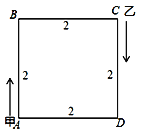
A.AB上B.BC上
C.CD上D.AD上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数![]() (a>0,a为常数)和
(a>0,a为常数)和![]() 在第一象限内的图象如图所示,点M在
在第一象限内的图象如图所示,点M在![]() 的图象上,MC丄x轴于点C,交
的图象上,MC丄x轴于点C,交![]() 的图象于点A,MD丄y轴于点D,交
的图象于点A,MD丄y轴于点D,交![]() 的图象于点B,当点M在
的图象于点B,当点M在![]() 的图象上运动时,以下结论:
的图象上运动时,以下结论:

①S△CDB=S△CCA
②四边形OAMB的面积为2-a
③当a=l时,点A是MC的中点
④若S四边形OAMB+S△CDB,则四边形OCMD为正方形.其中正确是________(把所有正确结论的序号写在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的边长为4,对角线相交于点P,顶点A、C分别在x轴、y轴的正半轴上,抛物线L经过0、P、A三点,点E是正方形内的抛物线上的动点.
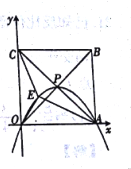
(1)点P的坐标为______
(2)求抛物线L的解析式.
(3)求△OAE与△OCE的面积之和的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细填一填:
把下列各数填入相应的大括号里:
5,-1,0,-6,+8,0.3,-![]() ,+
,+![]() ,-0.72,…
,-0.72,…
① 正数集合:{ __________________ …}
② 整数集合:{__________________…}
③ 负数集合:{ __________________ …}
④ 分数集合:{__________________ …}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com