
【题目】已知反比例函数y=![]() 的图象与一次函数y=kx+m的图象相交于点A(2,1).
的图象与一次函数y=kx+m的图象相交于点A(2,1).
(1)分别求出这两个函数的解析式;
(2)当x取什么范围时,反比例函数值大于0;
(3)若一次函数与反比例函数另一交点为B,且纵坐标为﹣4,当x取什么范围时,反比例函数值大于一次函数的值;
(4)试判断点P(﹣1,5)关于x轴的对称点P′是否在一次函数y=kx+m的图象上.
【答案】(1)y=![]() ,y=2x﹣3;(2)x>0;(3)x<﹣0.5或0<x<2;(4)点P′在直线上.
,y=2x﹣3;(2)x>0;(3)x<﹣0.5或0<x<2;(4)点P′在直线上.
【解析】试题分析:(1)根据题意,反比例函数y=![]() 的图象过点A(2,1),可求得k的值,进而可得解析式;一次函数y=kx+m的图象过点A(2,1),代入求得m的值,从而得出一次函数的解析式;(2)根据(1)中求得的解析式,当y>0时,解得对应x的取值即可;
的图象过点A(2,1),可求得k的值,进而可得解析式;一次函数y=kx+m的图象过点A(2,1),代入求得m的值,从而得出一次函数的解析式;(2)根据(1)中求得的解析式,当y>0时,解得对应x的取值即可;
(3)由题意可知,反比例函数值大于一次函数的值,即可得![]() >2x﹣3,解得x的取值范围即可;
>2x﹣3,解得x的取值范围即可;
(4)先根据题意求出P′的坐标,再代入一次函数的解析式即可判断P′是否在一次函数y=kx+m的图象上..
试题解析:解:(1)根据题意,反比例函数y=![]() 的图象与一次函数y=kx+m的图象相交于点A(2,1),
的图象与一次函数y=kx+m的图象相交于点A(2,1),
则反比例函数y=![]() 中有k=2×1=2,
中有k=2×1=2,
y=kx+m中,k=2,
又∵过(2,1),解可得m=﹣3;
故其解析式为y=![]() ,y=2x﹣3;
,y=2x﹣3;
(2)由(1)可得反比例函数的解析式为y=![]() ,
,
令y>0,即![]() >0,解可得x>0.
>0,解可得x>0.
(3)根据题意,要反比例函数值大于一次函数的值,
即![]() >2x﹣3,解可得x<﹣0.5或0<x<2.
>2x﹣3,解可得x<﹣0.5或0<x<2.
(4)根据题意,易得点P(﹣1,5)关于x轴的对称点P′的坐标为(﹣1,﹣5)
在y=2x﹣3中,x=﹣1时,y=﹣5;
故点P′在直线上.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为表彰在某活动中表现积极的同学,老师决定购买文具盒与钢笔作为奖品.已知5个文具盒、2支钢笔共需100元;3个文具盒、1支钢笔共需57元.
(1)每个文具盒、每支钢笔各多少元?
(2)若本次表彰活动,老师决定购买10件作为奖品,若购买![]() 个文具盒,10件奖品共需
个文具盒,10件奖品共需![]() 元,求
元,求![]() 与
与![]() 的函数关系式.如果至少需要购买3个文具盒,本次活动老师最多需要花多少钱?
的函数关系式.如果至少需要购买3个文具盒,本次活动老师最多需要花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,CD=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.

(1)求证:①△ABG≌△AFG; ②求GC的长;
(2)求△FGC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B'点,AE是折痕。

(1)试判断B'E与DC的位置关系并说明理由。
(2)如果∠C=130°,求∠AEB的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
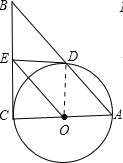
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为![]() ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)首先连接OD,由OE∥AB,根据平行线与等腰三角形的性质,易证得![]() ≌
≌![]() 即可得
即可得![]() ,则可证得
,则可证得![]() 为
为![]() 的切线;
的切线;
(2)连接CD,根据直径所对的圆周角是直角,即可得![]() 利用勾股定理即可求得
利用勾股定理即可求得![]() 的长,又由OE∥AB,证得
的长,又由OE∥AB,证得![]() 根据相似三角形的对应边成比例,即可求得
根据相似三角形的对应边成比例,即可求得![]() 的长,然后利用三角函数的知识,求得
的长,然后利用三角函数的知识,求得![]() 与
与![]() 的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
试题解析:(1)证明:连接OD,
∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
![]()
∴ED⊥OD,
∴ED是![]() 的切线;
的切线;
(2)连接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,
![]()
∵OE∥AB,
∴△COE∽△CAB,
![]() ∴AB=5,
∴AB=5,
∵AC是直径,
![]()
![]()
![]()
![]()
∵EF∥AB,
![]()
![]()
![]()
∴S△ADF=S梯形ABEFS梯形DBEF
![]()
∴△ADF的面积为![]()

【题型】解答题
【结束】
25
【题目】【题目】已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
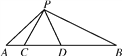
【题目】如图,点C,D在线段AB上,△PCD是等边三角形.
(1)当AC,CD,DB满足怎样的关系时,△ACP∽△PDB?
(2)当△ACP∽△PDB时,求∠APB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,假分数可以化为整数与真分数的和的形式.例如:![]() .在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如:像
.在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.例如:像![]() ,
,![]() ,…这样的分式是假分式;像
,…这样的分式是假分式;像![]() ,
,![]() ,…这样的分式是真分式.类似的,假分式也可以化为整式与真分式的和的形式. 例如:
,…这样的分式是真分式.类似的,假分式也可以化为整式与真分式的和的形式. 例如: ![]() ’
’
![]() .
.
(1)将分式![]() 化为整式与真分式的和的形式;
化为整式与真分式的和的形式;
(2)如果分式![]() 的值为整数,求x的整数值.
的值为整数,求x的整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假设北碚万达广场地下停车场有5个出入口,每天早晨6点开始对外停车且此时车位空置率为75%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满.2019年元旦节期间,由于商场人数增多,早晨6点时的车位空置率变为60%,又因为车库改造,只能开放2个进口和1个出口,则从早晨6点开始经过________小时车库恰好停满.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com