
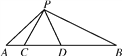
【题目】如图,点C,D在线段AB上,△PCD是等边三角形.
(1)当AC,CD,DB满足怎样的关系时,△ACP∽△PDB?
(2)当△ACP∽△PDB时,求∠APB的度数.
【答案】(1) CD2=AC·DB时,△ACP∽△PDB.
(2) 120°.
【解析】试题分析:(1)由△PCD是等边三角形可得∠ACP=∠PDB=120°,当![]() =
=![]() ,即
,即![]() =
=![]() ,即当CD2=AC·DB时,△ACP∽△PDB;(2)由△ACP∽△PDB可得∠A=∠DPB,所以∠APB=∠APC+∠CPD+∠DPB=∠APC+∠CPD+∠A=∠PCD+∠CPD=120°.
,即当CD2=AC·DB时,△ACP∽△PDB;(2)由△ACP∽△PDB可得∠A=∠DPB,所以∠APB=∠APC+∠CPD+∠DPB=∠APC+∠CPD+∠A=∠PCD+∠CPD=120°.
试题解析:
(1)∵△PCD是等边三角形,
∴∠ACP=∠PDB=120°.
当![]() =
=![]() ,即
,即![]() =
=![]() ,即当CD2=AC·DB时,△ACP∽△PDB.
,即当CD2=AC·DB时,△ACP∽△PDB.
(2)∵△ACP∽△PDB,∴∠A=∠DPB.
∴∠APB=∠APC+∠CPD+∠DPB=∠APC+∠CPD+∠A=∠PCD+∠CPD=120°.


科目:初中数学 来源: 题型:
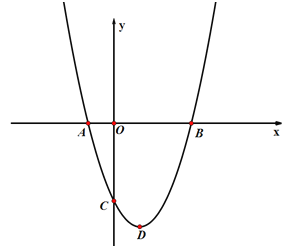
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于A、B两点(点A在点B的左侧),点B的坐标为(3,0),与
轴交于A、B两点(点A在点B的左侧),点B的坐标为(3,0),与![]() 轴交于点C(0,-3),顶点为D.
轴交于点C(0,-3),顶点为D.
(1)求抛物线的解析式及顶点D的坐标.
(2)联结AC,BC,求∠ACB的正切值.
(3)点P是x轴上一点,是否存在点P使得△PBD与△CAB相似,若存在,请求出点P的坐标;若不存在,请说明理由.
(4)M是抛物线上一点,点N在![]() 轴,是否存在点N,使得以点A,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
轴,是否存在点N,使得以点A,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:△ABC的周长为30cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边与点E,连接AD,若AE=4cm,则△ABD的周长是( )

A. 22cmB. 20cmC. 18cmD. 15cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,CE平分∠ACB,交BD于点E.下列结论:①BD是∠ABC的角平分线;②ΔBCD是等腰三角形;③BE=CD;④ΔAMD≌ΔBCD;⑤图中的等腰三角形有5个。其中正确的结论是___.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小伟遇到这样一个问题:如图1,在△ABC(其中∠BAC是一个可以变化的角)中,AB=2,AC=4,以BC为边在BC的下方作等边△PBC,求AP的最大值.
小伟是这样思考的:利用变换和等边三角形将边的位置重新组合.他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A′BC,连接A′A,当点A落在A′C上时,此题可解(如图2).
请你回答:AP的最大值是 .
参考小伟同学思考问题的方法,解决下列问题:
如图3,等腰Rt△ABC.边AB=4,P为△ABC内部一点,则AP+BP+CP的最小值是 .(结果可以不化简)

查看答案和解析>>
科目:初中数学 来源: 题型:
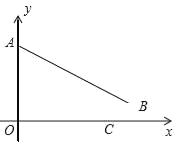
【题目】如图平面直角坐标系中,已知三点 A(0,7),B(8,1),C(x,0)且 0<x <8.
(1)求线段 AB 的长;
(2)请用含 x 的代数式表示 AC+BC 的值;
(3)求 AC+BC 的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
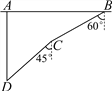
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com