
【题目】如图,已知AB=AC,∠A=36°,AB的中垂线MN交AC于点D,交AB于点M,CE平分∠ACB,交BD于点E.下列结论:①BD是∠ABC的角平分线;②ΔBCD是等腰三角形;③BE=CD;④ΔAMD≌ΔBCD;⑤图中的等腰三角形有5个。其中正确的结论是___.(填序号)

【答案】①②③⑤
【解析】
首先由AB的中垂线MD交AC于点D、交AB于点M,求得△ABD是等腰三角形,即可求得∠ABD的度数,又由AB=AC,即可求得∠ABC与∠C的度数,则可求得所有角的度数,进而得出BD是∠ABC的角平分线,可得△BCD也是等腰三角形,BE=CE,ΔBCD是等腰三角形,ΔAMD为直角三角形,故这两个三角形不可能全等,由角的度数即可得图中的等腰三角形.
解:∵AB=AC,∠A=36°,
∴∠ABC=∠ACB=72°
又∵CE平分∠ACB,
∴∠DCE=∠BCE=36°
又∵AB的中垂线MN交AC于点D,交AB于点M,
∴∠AMD=∠BMD=90°,AD=BD,
∴∠ABD=∠BAD=36°,∠ADB=108°,
又∵∠ADB=∠ACB+∠DBC=108°
∴∠DBC=36°
∠ABD=∠DBC,
∴BD是∠ABC的角平分线,
故①结论正确.
∠BDC=72°=∠ACB,
∴ΔBCD是等腰三角形,
故②结论正确.
∵∠DBC=∠ECB=36°
∴△BEC为等腰三角形,
∴BE=CE
又∵∠BDC=∠CED=72°
∴△DCE为等腰三角形,
∴CD=CE
∴BE=CD
故③结论正确.
∵ΔBCD是等腰三角形,ΔAMD为直角三角形
∴这两个三角形不可能全等,
故④结论错误.
图中△ABC、△ADB、△BCD、△BEC、△DCE都为等腰三角形,故⑤结论正确.
故本题正确的结论是①②③⑤.


科目:初中数学 来源: 题型:
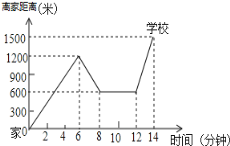
【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米;
(2)小明在书店停留了多少分钟;
(3)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司研发1000件新产品,需要精加工后才能投放市场.现在甲、乙两个工厂加工这批产品,已知甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天,而乙工厂每天加工的件数是甲工厂每天加工件数的1.25倍,公司需付甲工厂加工费用每天100元,乙工厂加工费用每天125元.
(1)甲、乙两个工厂每天各能加工多少件新产品?
(2)两个工厂同时合作完成这批产品,共付加工费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=120°,OP平分∠AOB,且OP=3,若点M,N分别在OA,OB上,ΔPMN为等边三角形,则满足上述条件的△PMN有中( )

A. 1个B. 2个C. 3个D. 3个以上
查看答案和解析>>
科目:初中数学 来源: 题型:
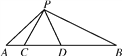
【题目】如图,点C,D在线段AB上,△PCD是等边三角形.
(1)当AC,CD,DB满足怎样的关系时,△ACP∽△PDB?
(2)当△ACP∽△PDB时,求∠APB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中装有9个黄球,13个黑球,11个红球,它们除颜色外其余都相同.
(1)求从袋中摸出一个球是红球的概率;
(2)现从袋中取出若干个黄球,井放入相同数量的黑球,若要使搅拌均与后从袋中摸出一个球是黑球的概率不小于![]() ,问至少要取出多少个黄球?
,问至少要取出多少个黄球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】★若两个扇形满足弧长的比等于它们半径的比,则称这两个扇形相似.如图,如果扇形AOB与扇形A1O1B1是相似扇形,且半径OA∶O1A1=k(k为不等于0的常数).那么下面四个结论:①∠AOB=∠A1O1B1;②△AOB∽△A1O1B1;③![]() =k;④扇形AOB与扇形A1O1B1的面积之比为k2.成立的个数为( )
=k;④扇形AOB与扇形A1O1B1的面积之比为k2.成立的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
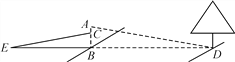
【题目】某一天,小明和小亮来到一河边,想用遮阳帽和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,先在河岸边选择了一点B(点B与河对岸岸边上的一棵树的底部点D所确定的直线垂直于河岸).
①小明在B点面向树的方向站好,调整帽檐,使视线通过帽檐正好落在树的底部点D处,如图所示,这时小亮测得小明眼睛距地面的距离AB=1.7米;
②小明站在原地转动180°后蹲下,并保持原来的观察姿态(除身体重心下移外,其他姿态均不变),这时视线通过帽檐落在了DB延长线上的点E处,此时小亮测得BE=9.6米,小明的眼睛距地面的距离CB=1.2米.
根据以上测量过程及测量数据,请你求出河宽BD是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某环保小组为了解世博园的游客在园区内购买瓶装饮料数量的情况,一天,他们分别在A、B、C三个出口处,对离开园区的游客进行调查,其中在A出口调查所得的数据整理后绘成如下图所示统计图:
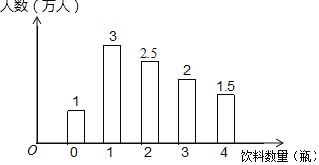
(1)在A出口的被调查游客中,购买瓶装饮料的数量的中位数是______瓶、众数是______瓶、平均数是______瓶;
(2)已知A、B、C三个出口的游客量比为2:2:1,用上面图表的人均购买饮料数量计算:这一天景区内若有50万游客,那么这一天购买的饮料的总数是多少?
表一:
出口 | B | C |
人均购买饮料数量(瓶) | 3 | 2 |
(3)若每瓶饮料要消耗0.5元处理包装的环保费用,该日需要花费多少钱处理这些饮料瓶?由此请你对游客做一点环保宣传建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com