
【题目】出租车司机小张某天下午的运营是在一条东西走向的大道上。如果规定向东为正,他这天下午的行程记录如下:(单位:千米)
+15,-3,+14,-11,+10,-18,+14
(1)将最后一名乘客送到目的地时,小张离下午出车点的距离是多少?
(2)离开下午出发点最远时是多少千米?
(3)若汽车的耗油量为0.06升/千米,油价为4.5元/升,这天下午共需支付多少油钱?
【答案】(1)东边21千米;(2)26千米;(3)22.95元.
【解析】
(1)把所有的行程数据相加即可求出小张离下午出车点的距离,若数据为正则在出发点的东边,反之在西边;
(2)分别计算出小张每一次行程离出发点的距离,再比较出各数据绝对值的大小即可;
(3)先计算出总路程,即为所走路程的绝对值的和,再利用耗油量![]() 每千米的耗油量
每千米的耗油量![]() 总路程,油钱=总耗油量×油的单价进行计算即可.
总路程,油钱=总耗油量×油的单价进行计算即可.
解:(1)小张离下午出车点的距离![]()
![]() (千米).
(千米).
答:将最后一名乘客送到目的地时,小张距下午出车时的出发点21千米,此时在出车点的东边;
(2)第一次:行程为![]() 千米时离开下午出发点+15千米;
千米时离开下午出发点+15千米;
第二次:行程为![]() 千米时离开下午出发点
千米时离开下午出发点![]() 千米;
千米;
第三次:行程为![]() 千米时离开下午出发点
千米时离开下午出发点![]() 千米;
千米;
第四次:行程为![]() 千米时离开下午出发点
千米时离开下午出发点![]() 千米;
千米;
第五次:行程为![]() 千米时离开下午出发点
千米时离开下午出发点![]() 千米;
千米;
第六次:行程为![]() 千米时离开下午出发点
千米时离开下午出发点![]() 千米;
千米;
第七次:行程为![]() 千米时离开下午出发点
千米时离开下午出发点![]() 千米;
千米;
![]() ,
,
![]() 离开下午出发点最远时是26千米,
离开下午出发点最远时是26千米,
答:离开下午出发点最远时是26千米;
(3)![]() 这天下午小张所走路程
这天下午小张所走路程![]()
![]()
![]() (千米),
(千米),
![]() 这天下午共需付钱
这天下午共需付钱![]() (元
(元![]() ,
,
答:这天下午共需支付22.95元油钱.


科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() 的图象与一次函数y=kx+m的图象相交于点A(2,1).
的图象与一次函数y=kx+m的图象相交于点A(2,1).
(1)分别求出这两个函数的解析式;
(2)当x取什么范围时,反比例函数值大于0;
(3)若一次函数与反比例函数另一交点为B,且纵坐标为﹣4,当x取什么范围时,反比例函数值大于一次函数的值;
(4)试判断点P(﹣1,5)关于x轴的对称点P′是否在一次函数y=kx+m的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的边长为4,对角线相交于点P,顶点A、C分别在x轴、y轴的正半轴上,抛物线L经过0、P、A三点,点E是正方形内的抛物线上的动点.
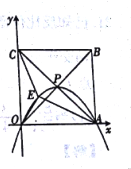
(1)点P的坐标为______
(2)求抛物线L的解析式.
(3)求△OAE与△OCE的面积之和的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意, 补全解题过程:
如图,∠AOB=90°,OE平分∠AOC,OF平分∠BOC. 求∠EOF的度数.
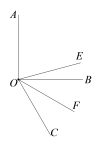
解:因为OE平分∠AOC,OF平分∠BOC
所以∠EOC =![]() ∠AOC,∠FOC =
∠AOC,∠FOC =![]() ________.
________.
所以∠EOF =∠EOC-________
=![]() (∠AOC-_______)
(∠AOC-_______)
=![]() ________
________
=_________°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细填一填:
把下列各数填入相应的大括号里:
5,-1,0,-6,+8,0.3,-![]() ,+
,+![]() ,-0.72,…
,-0.72,…
① 正数集合:{ __________________ …}
② 整数集合:{__________________…}
③ 负数集合:{ __________________ …}
④ 分数集合:{__________________ …}
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过学习绝对值,我们知道![]() 的几何意义是数轴上表示数
的几何意义是数轴上表示数![]() 在数轴上的对应点与原点的距离,如:
在数轴上的对应点与原点的距离,如:![]() 表示
表示![]() 在数轴上的对应点到原点的距离.
在数轴上的对应点到原点的距离.![]() ,即
,即![]() 表示
表示![]() 、
、![]() 在数轴上对应的两点之间的距离,类似的,
在数轴上对应的两点之间的距离,类似的,![]() ,即
,即![]() 表示
表示![]() 、
、![]() 在数轴上对应的两点之间的距离;一般地,点
在数轴上对应的两点之间的距离;一般地,点![]() ,
,![]() 在数轴上分别表示数
在数轴上分别表示数![]() 、
、![]() ,那么
,那么![]() ,
,![]() 之间的距离可表示为
之间的距离可表示为![]() .
.
请根据绝对值的几何意义并结合数轴解答下列问题:
(1)数轴上表示![]() 和
和![]() 的两点之间的距离是___;数轴上
的两点之间的距离是___;数轴上![]() 、
、![]() 两点的距离为
两点的距离为![]() ,点
,点![]() 表示的数是
表示的数是![]() ,则点
,则点![]() 表示的数是___.
表示的数是___.
(2)点![]() ,
,![]() ,
,![]() 在数轴上分别表示数
在数轴上分别表示数![]() 、
、![]() 、
、![]() ,那么
,那么![]() 到点
到点![]() .点
.点![]() 的距离之和可表示为_ (用含绝对值的式子表示);若
的距离之和可表示为_ (用含绝对值的式子表示);若![]() 到点
到点![]() .点
.点![]() 的距离之和有最小值,则
的距离之和有最小值,则![]() 的取值范围是_ __.
的取值范围是_ __.
(3)![]() 的最小值为_ __.
的最小值为_ __.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.

(1)求证:CF=DG;
(2)求出∠FHG的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com