
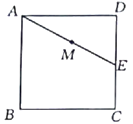
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 为
为![]() 边上一点,
边上一点,![]() ,点
,点![]() 为
为![]() 的中点,过点
的中点,过点![]() 作直线分别与
作直线分别与![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() .若
.若![]() ,则
,则![]() 长为______
长为______![]() .
.
【答案】1或2
【解析】
根据题意画出图形,过P作PN⊥BC,交BC于点N,由ABCD为正方形,得到AD=DC=PN,在直角三角形ADE中,利用锐角三角函数定义求出DE的长,进而利用勾股定理求出AE的长,根据M为AE中点求出AM的长,利用HL得到三角形ADE与三角形PQN全等,利用全等三角形对应边,对应角相等得到DE=NQ,∠DAE=∠NPQ=30°,再由PN与DC平行,得到∠PFA=∠DEA=60°,进而得到PM垂直于AE,在直角三角形APM中,根据AM的长,利用锐角三角函数定义求出AP的长,再利用对称性确定出AP′的长即可.
根据题意画出图形,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,四边形
,四边形![]() 为正方形,
为正方形,![]() .
.
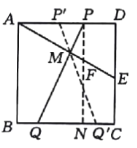
在![]() 中,
中,![]() ,
,![]() cm,
cm,
![]() cm.
cm.
根据勾股定理得![]() cm.
cm.
![]() 为
为![]() 的中点,
的中点,![]() cm,
cm,
在![]() 和
和![]() 中,
中,![]()
![]() ,
,
![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]() ,即
,即![]() .
.
在![]() 中,
中,![]() ,
, cm.
cm.
由对称性得到![]() cm,
cm,
综上,![]() 等于1cm或2cm.
等于1cm或2cm.
故答案为:1或2.


科目:初中数学 来源: 题型:
【题目】某市水果批发部门欲将 A 市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为 200 元/ 时.其它主要参考数据如下:
运输工具 | 途中平均速度(千米/ 时) | 运费(元/ 千米) | 装卸费用(元) |
火车 | 100 | 15 | 2000 |
汽车 | 80 | 20 | 900 |
运输过程中,火车因多次临时停车,全程在路上耽误 2 小时 45 分钟,火车的总支出费用与汽车的总支出费用相同,请问某市与本地的路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
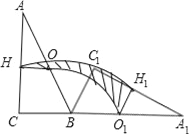
【题目】勾股定理是几何学中的明珠,充满着魅力,千百年来,人们对它趋之若鹜,其中有著名的数学家,也有业余数学爱好者,向常春在1994年构造发现了一个新的证法:把两个全等的直角三角形如图1放置,其三边长分别为a、b、c,显然∠DAB=∠B=90°,AC⊥DE.
(1)请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再通过探究这三个图形面积之间的关系,证明:勾股定理a2+b2=c2;
(2)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=24千米,BC=16千米,在AB上有一个供应站P,且PC=PD,求出AP的距离;
(3)借助(2)的思考过程与几何模型,直接写出代数式![]() 的最小值为 .
的最小值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠CAB=30°,BC=2,O、H分别为边AB、AC的中点,将△ABC绕点B顺时针旋转120°到△A1BC1的位置,则整个旋转过程中线段OH所扫过部分的面积(即阴影部分面积)为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小张某天下午的运营是在一条东西走向的大道上。如果规定向东为正,他这天下午的行程记录如下:(单位:千米)
+15,-3,+14,-11,+10,-18,+14
(1)将最后一名乘客送到目的地时,小张离下午出车点的距离是多少?
(2)离开下午出发点最远时是多少千米?
(3)若汽车的耗油量为0.06升/千米,油价为4.5元/升,这天下午共需支付多少油钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区一电瓶小客车接到任务从景区大门出发,向东走2千米到达A景区,继续向东走2.5千米到达B景区,然后又回头向西走8.5千米到达C景区,最后回到景区大门.
![]()
(1)以景区大门为原点,向东为正方向,以1个单位长表示1千米,建立如图所示的数轴,请在数轴上表示出上述A、B、C三个景区的位置.
(2)A景区与C景区之间的距离是多少?
(3)若电瓶车充足一次电能行走15千米,则该电瓶车能否在一开始充足电而途中不充电的情况下完成此次任务?请计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“直角”在初中数学学习中无处不在在数学活动课上,李老师要求同学们用所学知识,利用无刻度的直尺和圆规判断“已知∠AOB“是不是直角.甲、乙两名同学各自给出不同的作法,来判断∠AOB是不是直角
甲:如图1,在OA、OB上分别取点CD,以C为圆心,CD长为半径画弧,交OB的反向延长线于点E,若OE=OD,则∠AOB=90°;
乙:如图2,在OA、OB上分别截取OM=4个单位长度,ON=3个单位长度,若MN=5个单位长度,则∠AOB=90°;
甲、乙两位同学作法正确的是( )
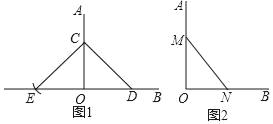
A. 甲正确,乙不正确B. 乙正确,甲不正确
C. 甲和乙都不正确D. 甲和乙都正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划选购甲、乙两种图书作为“校园读书节”的奖品.已知甲图书的单价是乙图书单价的![]() 倍;用
倍;用![]() 元单独购买甲种图书比单独购买乙种图书要少
元单独购买甲种图书比单独购买乙种图书要少![]() 本.
本.
(1)甲、乙两种图书的单价分别为多少元?
(2)若学校计划购买这两种图书共![]() 本,且投入的经费不超过
本,且投入的经费不超过![]() 元,要使购买的甲种图书数量不少于乙种图书的数量,则共有几种购买方案?
元,要使购买的甲种图书数量不少于乙种图书的数量,则共有几种购买方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com