
【题目】如图,已知平行四边形![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() 与
与![]() 交于
交于![]() 点.
点.
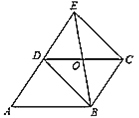
(1)求证:![]() ;
;
(2)当![]() 时,连续
时,连续![]() ,
,![]() ,求证:四边形
,求证:四边形![]() 为矩形.
为矩形.
【答案】(1)详见解析;(2)见解析.
【解析】
(1)根据平行四边形性质得出AD=BC,AD∥BC,推出∠EDO=∠BCO,∠DEO=∠CBO,求出DE=BC,根据ASA推出两三角形全等即可;
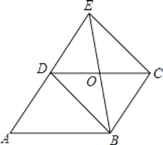
(2)求出∠EDO=∠A=![]() ∠EOC,推出∠ODE=∠OED,推出OD=OE,得出平行四边形BCED,推出CD=BE,根据矩形的判定推出即可.
∠EOC,推出∠ODE=∠OED,推出OD=OE,得出平行四边形BCED,推出CD=BE,根据矩形的判定推出即可.
证明:(1)∵在平行四边形ABCD中,
AD=BC,AD∥BC,
∴∠EDO=∠BCO,∠DEO=∠CBO,
∵DE=AD,
∴DE=BC,
在△BOC和△EOD中
∵ ,
,
∴△BOC≌△EOD(ASA);
(2)∵DE=BC,DE∥BC,
∴四边形BCED是平行四边形,
在平行四边形ABCD中,AB∥DC,
∴∠A=∠ODE,
∵∠A=![]() ∠EOC,
∠EOC,
∴∠ODE=![]() ∠EOC,
∠EOC,
∵∠ODE+∠OED=∠EOC,
∴∠ODE=∠OED,
∴OE=OD,
∵平行四边形BCED中,CD=2OD,BE=2OE,
∴CD=BE,
∴平行四边形BCED为矩形.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】正方形ABCD的轨道上有两个点甲与乙,开始时甲在A处,乙在C处,它们沿着正方形轨道顺时针同时出发,甲的速度为每秒1 cm,乙的速度为每秒5 cm,已知正方形轨道ABCD的边长为2 cm,则乙在第2 020次追上甲时的位置在( )
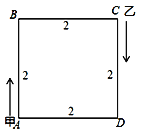
A.AB上B.BC上
C.CD上D.AD上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意, 补全解题过程:
如图,∠AOB=90°,OE平分∠AOC,OF平分∠BOC. 求∠EOF的度数.
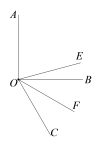
解:因为OE平分∠AOC,OF平分∠BOC
所以∠EOC =![]() ∠AOC,∠FOC =
∠AOC,∠FOC =![]() ________.
________.
所以∠EOF =∠EOC-________
=![]() (∠AOC-_______)
(∠AOC-_______)
=![]() ________
________
=_________°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细填一填:
把下列各数填入相应的大括号里:
5,-1,0,-6,+8,0.3,-![]() ,+
,+![]() ,-0.72,…
,-0.72,…
① 正数集合:{ __________________ …}
② 整数集合:{__________________…}
③ 负数集合:{ __________________ …}
④ 分数集合:{__________________ …}
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)如图①,若点E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图②,若∠EAF=60°,求证:△AEF是等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过学习绝对值,我们知道![]() 的几何意义是数轴上表示数
的几何意义是数轴上表示数![]() 在数轴上的对应点与原点的距离,如:
在数轴上的对应点与原点的距离,如:![]() 表示
表示![]() 在数轴上的对应点到原点的距离.
在数轴上的对应点到原点的距离.![]() ,即
,即![]() 表示
表示![]() 、
、![]() 在数轴上对应的两点之间的距离,类似的,
在数轴上对应的两点之间的距离,类似的,![]() ,即
,即![]() 表示
表示![]() 、
、![]() 在数轴上对应的两点之间的距离;一般地,点
在数轴上对应的两点之间的距离;一般地,点![]() ,
,![]() 在数轴上分别表示数
在数轴上分别表示数![]() 、
、![]() ,那么
,那么![]() ,
,![]() 之间的距离可表示为
之间的距离可表示为![]() .
.
请根据绝对值的几何意义并结合数轴解答下列问题:
(1)数轴上表示![]() 和
和![]() 的两点之间的距离是___;数轴上
的两点之间的距离是___;数轴上![]() 、
、![]() 两点的距离为
两点的距离为![]() ,点
,点![]() 表示的数是
表示的数是![]() ,则点
,则点![]() 表示的数是___.
表示的数是___.
(2)点![]() ,
,![]() ,
,![]() 在数轴上分别表示数
在数轴上分别表示数![]() 、
、![]() 、
、![]() ,那么
,那么![]() 到点
到点![]() .点
.点![]() 的距离之和可表示为_ (用含绝对值的式子表示);若
的距离之和可表示为_ (用含绝对值的式子表示);若![]() 到点
到点![]() .点
.点![]() 的距离之和有最小值,则
的距离之和有最小值,则![]() 的取值范围是_ __.
的取值范围是_ __.
(3)![]() 的最小值为_ __.
的最小值为_ __.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】夏师傅是一名徒步运动的爱好者,他用手机软件记录了某个月(30天)每天徒步的步数(单位:万步),将记录结果绘制成了如图所示的统计图.在这组徒步数据中,众数和中位数分别是( )

A. 1.2,1.3 B. 1.4,1.3 C. 1.4,1.35 D. 1.3,1.3
查看答案和解析>>
科目:初中数学 来源: 题型:
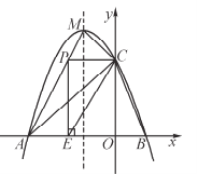
【题目】如图,抛物线![]() 与
与![]() 轴交于A、B两点,与y轴交于点C(0,3),且此抛物线的顶点坐标为M(-1,4).
轴交于A、B两点,与y轴交于点C(0,3),且此抛物线的顶点坐标为M(-1,4).
(1)求此抛物线的解析式;
(2)设点D为已知抛物线对称轴上的任意一点,当△ACD面积等于6时,求点D的坐标;
(3)点P在线段AM上,当PC与y轴垂直时,过点P作![]() 轴的垂线,垂足为E,将△PCE沿直线CB翻折,使点P的对应点P'与P、E、C处在同一平面内,请求出P'坐标,并判断点P'是否在抛物线上.
轴的垂线,垂足为E,将△PCE沿直线CB翻折,使点P的对应点P'与P、E、C处在同一平面内,请求出P'坐标,并判断点P'是否在抛物线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com