
【题目】通过学习绝对值,我们知道![]() 的几何意义是数轴上表示数
的几何意义是数轴上表示数![]() 在数轴上的对应点与原点的距离,如:
在数轴上的对应点与原点的距离,如:![]() 表示
表示![]() 在数轴上的对应点到原点的距离.
在数轴上的对应点到原点的距离.![]() ,即
,即![]() 表示
表示![]() 、
、![]() 在数轴上对应的两点之间的距离,类似的,
在数轴上对应的两点之间的距离,类似的,![]() ,即
,即![]() 表示
表示![]() 、
、![]() 在数轴上对应的两点之间的距离;一般地,点
在数轴上对应的两点之间的距离;一般地,点![]() ,
,![]() 在数轴上分别表示数
在数轴上分别表示数![]() 、
、![]() ,那么
,那么![]() ,
,![]() 之间的距离可表示为
之间的距离可表示为![]() .
.
请根据绝对值的几何意义并结合数轴解答下列问题:
(1)数轴上表示![]() 和
和![]() 的两点之间的距离是___;数轴上
的两点之间的距离是___;数轴上![]() 、
、![]() 两点的距离为
两点的距离为![]() ,点
,点![]() 表示的数是
表示的数是![]() ,则点
,则点![]() 表示的数是___.
表示的数是___.
(2)点![]() ,
,![]() ,
,![]() 在数轴上分别表示数
在数轴上分别表示数![]() 、
、![]() 、
、![]() ,那么
,那么![]() 到点
到点![]() .点
.点![]() 的距离之和可表示为_ (用含绝对值的式子表示);若
的距离之和可表示为_ (用含绝对值的式子表示);若![]() 到点
到点![]() .点
.点![]() 的距离之和有最小值,则
的距离之和有最小值,则![]() 的取值范围是_ __.
的取值范围是_ __.
(3)![]() 的最小值为_ __.
的最小值为_ __.
【答案】(1)2,1或7;(2)|x+1|+|x-2|,-1≤x≤2;(3)3
【解析】
(1)根据数轴上A、B两点之间的距离|AB|=|a-b|.代入数值运用绝对值即可求任意两点间的距离.
(2)根据数轴上两点之间的距离公式可求A到B的距离与A到C的距离之和;满足|x-3|+|x+2|=7的x的值,分三种情形讨论,转化为方程解决问题;
(3)当1≤x≤4时,|x-1|+|x-4|有最小值为|4-1|=3.
解:(1)数轴上表示2和4的两点之间的距离是4-2=2;
数轴上P、Q两点的距离为3,点P表示的数是4,则点Q表示的数是4-3=1或4+3=7;
(2)A到B的距离与A到C的距离之和,可表示为|x+1|+|x-2|,
∵|x-3|+|x+2|=7,当x<-1时,|x+1|+|x-2|=2-x-x-1=1-2x无最小值,
当-1≤x≤2时,|x+1|+|x-2|=x+1+2-x=3,
当x>2时,x+1+x-2=2x-1>3,
故若A到点B、点C的距离之和有最小值,则x的取值范围是-1≤x≤2;
(3)原式=|x-1|+|x-4|.
当1≤x≤4时,|x-1|+|x-4|有最小值为|4-1|=3
故答案为:(1)2,1或7;(2)|x+1|+|x-2|,-1≤x≤2;(3)3


科目:初中数学 来源: 题型:
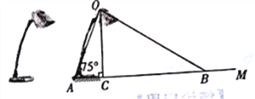
【题目】图为放置在水平桌面上的台灯的平面示意图,可伸缩式灯臂AO长为40 cm,与水平面所形成的夹角∠OAM恒为75°(不受灯臂伸缩的影响).由光源0射出的光线沿灯罩形成光线OC,OB,与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°.
(1)求该台灯照亮桌面的宽度BC.(不考虑其他因素,结果精确到1 cm,参考数据:sin75°≈0.97,cos75°≈0.26, ![]() ≈1.73)
≈1.73)
(2)若灯臂最多可伸长至60 cm,不调整灯罩的角度,能否让台灯照亮桌面85 cm的宽度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小张某天下午的运营是在一条东西走向的大道上。如果规定向东为正,他这天下午的行程记录如下:(单位:千米)
+15,-3,+14,-11,+10,-18,+14
(1)将最后一名乘客送到目的地时,小张离下午出车点的距离是多少?
(2)离开下午出发点最远时是多少千米?
(3)若汽车的耗油量为0.06升/千米,油价为4.5元/升,这天下午共需支付多少油钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明元旦节吃完晚饭后6点过还没到7点,他陪他妈到成华区SM广场去买东西,离家时他发现他家的时钟上时针与分针刚好重合,他离家的时间是_______(用几点几分几秒表示,注意“四舍五入”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“直角”在初中数学学习中无处不在在数学活动课上,李老师要求同学们用所学知识,利用无刻度的直尺和圆规判断“已知∠AOB“是不是直角.甲、乙两名同学各自给出不同的作法,来判断∠AOB是不是直角
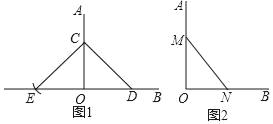
甲:如图1,在OA、OB上分别取点CD,以C为圆心,CD长为半径画弧,交OB的反向延长线于点E,若OE=OD,则∠AOB=90°;
乙:如图2,在OA、OB上分别截取OM=4个单位长度,ON=3个单位长度,若MN=5个单位长度,则∠AOB=90°;
甲、乙两位同学作法正确的是( )
A. 甲正确,乙不正确B. 乙正确,甲不正确
C. 甲和乙都不正确D. 甲和乙都正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:菱形ABCD中,∠B=60°,将含60°角的直角三角板的60°角的顶点放到菱形ABCD的顶点A处,两边分别与菱形的边BC,CD交于点F,E.
(1)(如图1)求证:AE=AF;
(2)连结EF,交AC于点H(如图2),试探究AB,AF,AH之间的关系;
(3)若AB=6,EF=2![]() ,且CE<DE,求FH的长.
,且CE<DE,求FH的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
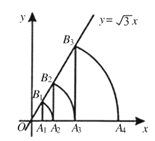
【题目】如图,已知直线y=![]() x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1的长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2的长为半径画弧交x轴于点A3,…,按此做法进行下去,则点A6的坐标为____________.
x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1的长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2的长为半径画弧交x轴于点A3,…,按此做法进行下去,则点A6的坐标为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB交x轴于点B(2,0),交y轴于点A(0,2),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=3,连接DA,∠DAC=90°.
(1)求直线AB的解析式.
(2)求D点坐标及过O、D、B三点的抛物线解析式.
(3)若点P是线段OB上的动点,过点P作x轴的垂线交AB于F,交(2)中抛物线于E,连CE,是否存在P使△BPF与△FCE相似?若存在,请求出P点坐标;若不存在说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com