
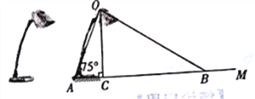
ЁОЬтФПЁПЭМЮЊЗХжУдкЫЎЦНзРУцЩЯЕФЬЈЕЦЕФЦНУцЪОвтЭМЃЌПЩЩьЫѕЪНЕЦБлAOГЄЮЊ40 cm,гыЫЎЦНУцЫљаЮГЩЕФМаНЧЁЯOAMКуЮЊ75Ёу(ВЛЪмЕЦБлЩьЫѕЕФгАЯь).гЩЙтдД0ЩфГіЕФЙтЯпбиЕЦежаЮГЩЙтЯпOCЃЌOBЃЌгыЫЎЦНУцЫљаЮГЩЕФМаНЧЁЯOCA,ЁЯOBAЗжБ№ЮЊ90ЁуКЭ30Ёу.
(1)ЧѓИУЬЈЕЦееССзРУцЕФПэЖШBC.(ВЛПМТЧЦфЫћвђЫиЃЌНсЙћОЋШЗЕН1 cmЃЌВЮПМЪ§Он:sin75ЁуЁж0.97,cos75ЁуЁж0.26ЃЌ ![]() Ёж1.73)
Ёж1.73)
(2)ШєЕЦБлзюЖрПЩЩьГЄжС60 cm,ВЛЕїећЕЦежЕФНЧЖШЃЌФмЗёШУЬЈЕЦееССзРУц85 cmЕФПэЖШ?
ЁОД№АИЁП(1) 67cm;(2) МћНтЮі
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉдк![]() жа,ЧѓЕУ
жа,ЧѓЕУ![]() дйдк
дйдк![]() жаЃЌгЩ
жаЃЌгЩ![]() ПЩЕУД№АИЃЛ
ПЩЕУД№АИЃЛ
ЃЈ2ЃЉНЋЃЈ1ЃЉжаЫљЕУНсЙћжа40ЬцЛЛГЩ60ЃЌМЦЫуМДПЩХаЖЯЃЎ
ЪдЬтНтЮіЃКЂХдк![]() жа,
жа, ![]() ,
,
ЙЪ![]()
дк![]() жа,
жа, ![]() ,ЙЪ
,ЙЪ![]() ЃЌ
ЃЌ
НтЕУBCЁж67,
Д№.ИУЬЈЕЦееССЫЎЦНСНЕФПэЖШBCДѓдМЪЧ67cm.
![]() ИљОнЬтвт,ШєOA=60cm,дђ
ИљОнЬтвт,ШєOA=60cm,дђ![]()
ЙЪЬЈЕЦПЩвдееССзРУц85cmЕФПэЖШ.
МДЬЈЕЦПЩвдееССзРУц85 cmЕФПэЖШ.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуOЮЊжБЯпABЩЯвЛЕуЃЌЙ§ЕуOзїжБЯпOCЃЌвбжЊЁЯAOCЁй90ЁуЃЌЩфЯпODЦНЗжЁЯAOCЃЌЩфЯпOEЦНЗжЁЯBOCЃЌЩфЯпOFЦНЗжЁЯDOEЃЎ

ЃЈ1ЃЉЧѓЁЯDOEКЭЁЯDOFЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШєЁЯDOC=3ЁЯCOFЃЌЧѓЁЯAOCЕФЖШЪ§ЃЛ
ЃЈ3ЃЉЧѓЁЯBOF+ЁЯDOCЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓгывЛДЮКЏЪ§y=kx+mЕФЭМЯѓЯрНЛгкЕуAЃЈ2ЃЌ1ЃЉЃЎ
ЕФЭМЯѓгывЛДЮКЏЪ§y=kx+mЕФЭМЯѓЯрНЛгкЕуAЃЈ2ЃЌ1ЃЉЃЎ
ЃЈ1ЃЉЗжБ№ЧѓГіетСНИіКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕБxШЁЪВУДЗЖЮЇЪБЃЌЗДБШР§КЏЪ§жЕДѓгк0ЃЛ
ЃЈ3ЃЉШєвЛДЮКЏЪ§гыЗДБШР§КЏЪ§СэвЛНЛЕуЮЊBЃЌЧвзнзјБъЮЊЉ4ЃЌЕБxШЁЪВУДЗЖЮЇЪБЃЌЗДБШР§КЏЪ§жЕДѓгквЛДЮКЏЪ§ЕФжЕЃЛ
ЃЈ4ЃЉЪдХаЖЯЕуPЃЈЉ1ЃЌ5ЃЉЙигкxжсЕФЖдГЦЕуPЁфЪЧЗёдквЛДЮКЏЪ§y=kx+mЕФЭМЯѓЩЯЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПе§ЗНаЮABCDЕФЙьЕРЩЯгаСНИіЕуМзгыввЃЌПЊЪМЪБМздкAДІЃЌввдкCДІЃЌЫќУЧбизХе§ЗНаЮЙьЕРЫГЪБеыЭЌЪБГіЗЂЃЌМзЕФЫйЖШЮЊУПУы1 cmЃЌввЕФЫйЖШЮЊУПУы5 cmЃЌвбжЊе§ЗНаЮЙьЕРABCDЕФБпГЄЮЊ2 cmЃЌдђввдкЕк2 020ДЮзЗЩЯМзЪБЕФЮЛжУдкЃЈЁЁЁЁЃЉ
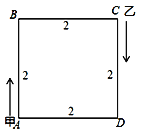
A.ABЩЯB.BCЩЯ
C.CDЩЯD.ADЩЯ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЗДБШР§КЏЪ§![]() ЃЈa>0,aЮЊГЃЪ§ЃЉКЭ
ЃЈa>0,aЮЊГЃЪ§ЃЉКЭ![]() дкЕквЛЯѓЯоФкЕФЭМЯѓШчЭМЫљЪОЃЌЕуMдк
дкЕквЛЯѓЯоФкЕФЭМЯѓШчЭМЫљЪОЃЌЕуMдк![]() ЕФЭМЯѓЩЯЃЌMCAxжсгкЕуCЃЌНЛ
ЕФЭМЯѓЩЯЃЌMCAxжсгкЕуCЃЌНЛ![]() ЕФЭМЯѓгкЕуAЃЌMDAyжсгкЕуDЃЌНЛ
ЕФЭМЯѓгкЕуAЃЌMDAyжсгкЕуDЃЌНЛ![]() ЕФЭМЯѓгкЕуBЃЌЕБЕуMдк
ЕФЭМЯѓгкЕуBЃЌЕБЕуMдк![]() ЕФЭМЯѓЩЯдЫЖЏЪБЃЌвдЯТНсТлЃК
ЕФЭМЯѓЩЯдЫЖЏЪБЃЌвдЯТНсТлЃК

ЂйSЁїCDB=SЁїCCA
ЂкЫФБпаЮOAMBЕФУцЛ§ЮЊ2-a
ЂлЕБa=lЪБЃЌЕуAЪЧMCЕФжаЕу
ЂмШєSЫФБпаЮOAMB+SЁїCDBЃЌдђЫФБпаЮOCMDЮЊе§ЗНаЮ.Цфжае§ШЗЪЧ________ЃЈАбЫљгае§ШЗНсТлЕФађКХаДдкКсЯпЩЯ)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбЇаЃвЊДгМзввСНУћЩфЛїдЫЖЏдБжаЬєбЁвЛШЫВЮМгШЋЪаБШШќЃЌдкбЁАЮШќжаЃЌУПШЫНјааСЫ5ДЮЩфЛїЃЌМзЕФГЩМЈЃЈЛЗЃЉЮЊЃК9.7ЃЌ10ЃЌ9.6ЃЌ9.8ЃЌ9.9ЃЛввЕФГЩМЈЕФЦНОљЪ§ЮЊ9.8ЃЌЗНВюЮЊ0.032ЃЛ
ЃЈ1ЃЉМзЕФЩфЛїГЩМЈЕФЦНОљЪ§КЭЗНВюЗжБ№ЪЧЖрЩйЃП
ЃЈ2ЃЉОнЙРМЦЃЌШчЙћГЩМЈЕФЦНОљЪ§ДяЕН9.8ЛЗОЭПЩФмЖсЕУН№ХЦЃЌЮЊСЫЖсЕУН№ХЦЃЌгІбЁЫВЮМгБШШќЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮOABCЕФБпГЄЮЊ4,ЖдНЧЯпЯрНЛгкЕуPЃЌЖЅЕуAЁЂCЗжБ№дкxжсЁЂyжсЕФе§АыжсЩЯЃЌХзЮяЯпLОЙ§0ЁЂPЁЂAШ§ЕуЃЌЕуEЪЧе§ЗНаЮФкЕФХзЮяЯпЩЯЕФЖЏЕу.
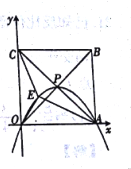
(1)ЕуPЕФзјБъЮЊ______
(2)ЧѓХзЮяЯпLЕФНтЮіЪН.
(3)ЧѓЁїOAEгыЁїOCEЕФУцЛ§жЎКЭЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИљОнЬтвтЃЌ ВЙШЋНтЬтЙ§ГЬЃК
ШчЭМЃЌЁЯAOB=90ЁуЃЌOEЦНЗжЁЯAOCЃЌOFЦНЗжЁЯBOCЃЎ ЧѓЁЯEOFЕФЖШЪ§.
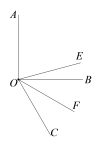
НтЃКвђЮЊOEЦНЗжЁЯAOCЃЌOFЦНЗжЁЯBOC
ЫљвдЁЯEOC =![]() ЁЯAOCЃЌЁЯFOC =
ЁЯAOCЃЌЁЯFOC =![]() ________.
________.
ЫљвдЁЯEOF =ЁЯEOC-________
=![]() (ЁЯAOC-_______)
(ЁЯAOC-_______)
=![]() ________
________
=_________Ёу.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭЈЙ§бЇЯАОјЖджЕ,ЮвУЧжЊЕР![]() ЕФМИКЮвтвхЪЧЪ§жсЩЯБэЪОЪ§
ЕФМИКЮвтвхЪЧЪ§жсЩЯБэЪОЪ§![]() дкЪ§жсЩЯЕФЖдгІЕугыдЕуЕФОрРы,ШчЃК
дкЪ§жсЩЯЕФЖдгІЕугыдЕуЕФОрРы,ШчЃК![]() БэЪО
БэЪО![]() дкЪ§жсЩЯЕФЖдгІЕуЕНдЕуЕФОрРы.
дкЪ§жсЩЯЕФЖдгІЕуЕНдЕуЕФОрРы.![]() ,МД
,МД![]() БэЪО
БэЪО![]() ЁЂ
ЁЂ![]() дкЪ§жсЩЯЖдгІЕФСНЕужЎМфЕФОрРы,РрЫЦЕФ,
дкЪ§жсЩЯЖдгІЕФСНЕужЎМфЕФОрРы,РрЫЦЕФ,![]() ЃЌМД
ЃЌМД![]() БэЪО
БэЪО![]() ЁЂ
ЁЂ![]() дкЪ§жсЩЯЖдгІЕФСНЕужЎМфЕФОрРыЃЛвЛАуЕиЃЌЕу
дкЪ§жсЩЯЖдгІЕФСНЕужЎМфЕФОрРыЃЛвЛАуЕиЃЌЕу![]() ЃЌ
ЃЌ![]() дкЪ§жсЩЯЗжБ№БэЪОЪ§
дкЪ§жсЩЯЗжБ№БэЪОЪ§![]() ЁЂ
ЁЂ![]() ЃЌФЧУД
ЃЌФЧУД![]() ЃЌ
ЃЌ![]() жЎМфЕФОрРыПЩБэЪОЮЊ
жЎМфЕФОрРыПЩБэЪОЮЊ![]() .
.
ЧыИљОнОјЖджЕЕФМИКЮвтвхВЂНсКЯЪ§жсНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЪ§жсЩЯБэЪО![]() КЭ
КЭ![]() ЕФСНЕужЎМфЕФОрРыЪЧ___ЃЛЪ§жсЩЯ
ЕФСНЕужЎМфЕФОрРыЪЧ___ЃЛЪ§жсЩЯ![]() ЁЂ
ЁЂ![]() СНЕуЕФОрРыЮЊ
СНЕуЕФОрРыЮЊ![]() ЃЌЕу
ЃЌЕу![]() БэЪОЕФЪ§ЪЧ
БэЪОЕФЪ§ЪЧ![]() ЃЌдђЕу
ЃЌдђЕу![]() БэЪОЕФЪ§ЪЧ___.
БэЪОЕФЪ§ЪЧ___.
ЃЈ2ЃЉЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() дкЪ§жсЩЯЗжБ№БэЪОЪ§
дкЪ§жсЩЯЗжБ№БэЪОЪ§![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ,ФЧУД
,ФЧУД![]() ЕНЕу
ЕНЕу![]() .Еу
.Еу![]() ЕФОрРыжЎКЭПЩБэЪОЮЊ_ (гУКЌОјЖджЕЕФЪНзгБэЪО)ЃЛШє
ЕФОрРыжЎКЭПЩБэЪОЮЊ_ (гУКЌОјЖджЕЕФЪНзгБэЪО)ЃЛШє![]() ЕНЕу
ЕНЕу![]() .Еу
.Еу![]() ЕФОрРыжЎКЭгазюаЁжЕЃЌдђ
ЕФОрРыжЎКЭгазюаЁжЕЃЌдђ![]() ЕФШЁжЕЗЖЮЇЪЧ_ __.
ЕФШЁжЕЗЖЮЇЪЧ_ __.
ЃЈ3ЃЉ![]() ЕФзюаЁжЕЮЊ_ __.
ЕФзюаЁжЕЮЊ_ __.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com