
【题目】如图,点O为直线AB上一点,过点O作直线OC,已知∠AOC≠90°,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE.

(1)求∠DOE和∠DOF的度数;
(2)若∠DOC=3∠COF,求∠AOC的度数;
(3)求∠BOF+∠DOC的度数.
【答案】(1)∠DOE=90°,∠DOF=45°;(2)∠AOC=67.5° ;(3)∠BOF+∠DOC=135°
【解析】
(1)根据 射线OD平分∠AOC,射线OE平分∠BOC,即可求出∠DOE,再根据OF平分∠DOE,即可求出∠DOF的度数;
(2),由∠DOC=3∠COF,得出∠DOC的度数,再根据OD平分∠AOC,即可求得∠AOC的度数.
(3)先根据射线OD平分∠AOC,∠AOD=∠COD,得到,![]() ,再根据∠AOC+∠BOC=180°,得出∠DOE=90°,由射线OF平分∠DOE,得∠DOF=∠EOF=45°,从而求得∠FOB+∠DOC的度数;
,再根据∠AOC+∠BOC=180°,得出∠DOE=90°,由射线OF平分∠DOE,得∠DOF=∠EOF=45°,从而求得∠FOB+∠DOC的度数;
(1)![]() ,
,
![]()
∴![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() .
.
(2)∵∠DOC=3∠COF,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵OD平分∠AOC,
∴![]() .
.
(3)∵OD平分∠AOC,∴![]() ,
,
∴![]()
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠BAC>90°,点D为BC的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连结AD,则下列结论不一定正确的是( )

A. AE=EF B. AB=2DE
C. △ADF和△ADE的面积相等 D. △ADE和△FDE的面积相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法:求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想转化,把未知转化为已知.用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程![]() ,可以通过因式分解把它转化为
,可以通过因式分解把它转化为![]() ,可得
,可得![]() ,所以x=0或x+2=0或x-1=0,所以方程:
,所以x=0或x+2=0或x-1=0,所以方程:![]() 的解是x1=0,x2=-2,x3=1;
的解是x1=0,x2=-2,x3=1;
(1)问题:用“转化”思想求方程![]() 的解
的解
(2)应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
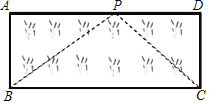
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某区为调查学生的视力变化情况,从全区九年级学生中抽取了部分学生,统计了每个人连续三年视力检查的结果,并将所得数据处理后,制成折线统计图和扇形统计图如下:
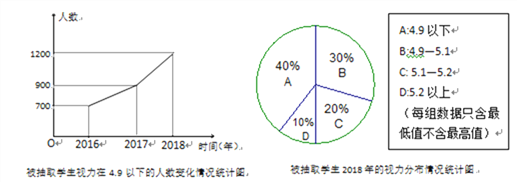
解答下列问题:
(1)该区共抽取了多少名九年级学生?
(2)若该区共有9万名九年级学生,请你估计2018年该区视力不良(4.9以下)的该年级学生大有多少人?
(3)扇形统计图中B的圆心角度数为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
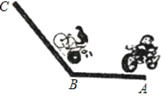
【题目】如图,现有两条乡村公路AB、BC,AB长为1200米,BC长为1600,一个人骑摩托车从A处以20m/s的速度匀速沿公路AB、BC向C处行驶;另一人骑自行车从B处以5m/s的速度从B向C行驶,并且两人同时出发.
(1)求经过多少秒摩托车追上自行车?
(2)求两人均在行驶途中时,经过多少秒两人在行进路线上相距150米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图6,在平面直角坐标系中,一次函数![]() =
=![]() +1的图象交
+1的图象交![]() 轴于点D,与反比例函数
轴于点D,与反比例函数![]() =
=![]() 的图象在第一象限相交于点A.过点A分别作
的图象在第一象限相交于点A.过点A分别作![]() 轴
轴![]() 轴的垂线,垂足为点BC.
轴的垂线,垂足为点BC.
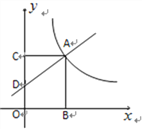
(1)点D的坐标为 ;
(2)当AB=4AC时,求![]() 值;
值;
(3)当四边形OBAC是正方形时,直接写出四边形ABOD与△ACD面积的比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,某交警巡逻车在东西方向的青年路上巡逻,他从岗亭![]() 出发,晚上停留在
出发,晚上停留在![]() 处.规定向东方向为正,向西方向为负,当天行驶情况记录如下(单位:千米):
处.规定向东方向为正,向西方向为负,当天行驶情况记录如下(单位:千米):
+5,-8,+10,-12,+6,-18,+5,-2.
(1)![]() 处在岗亭
处在岗亭![]() 的什么方向?距离岗亭
的什么方向?距离岗亭![]() 多远?
多远?
(2)若巡逻车每行驶1千米耗油0.1升,这一天共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
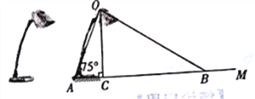
【题目】图为放置在水平桌面上的台灯的平面示意图,可伸缩式灯臂AO长为40 cm,与水平面所形成的夹角∠OAM恒为75°(不受灯臂伸缩的影响).由光源0射出的光线沿灯罩形成光线OC,OB,与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°.
(1)求该台灯照亮桌面的宽度BC.(不考虑其他因素,结果精确到1 cm,参考数据:sin75°≈0.97,cos75°≈0.26, ![]() ≈1.73)
≈1.73)
(2)若灯臂最多可伸长至60 cm,不调整灯罩的角度,能否让台灯照亮桌面85 cm的宽度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com