
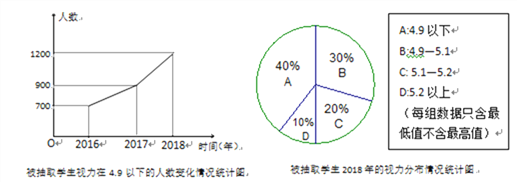
【题目】我市某区为调查学生的视力变化情况,从全区九年级学生中抽取了部分学生,统计了每个人连续三年视力检查的结果,并将所得数据处理后,制成折线统计图和扇形统计图如下:
解答下列问题:
(1)该区共抽取了多少名九年级学生?
(2)若该区共有9万名九年级学生,请你估计2018年该区视力不良(4.9以下)的该年级学生大有多少人?
(3)扇形统计图中B的圆心角度数为____.
【答案】(1) 3000名;(2) 36000人视力不良; (3)108.
【解析】分析:
(1)由两幅统计图中的信息可知,2018年视力在4.9以下的有1200人,占被抽查人数的40%,由此即可计算出2018年被抽查学生的总数了;
(2)由扇形统计图可知,视力在4.9以下的占了总数的40%,由此即可计算出90000名学生中共有多少人的视力在4.9以下;
(3)由图中数据可知,扇形统计图中B部分所对应圆心角为:360°×30%=108°.
详解:
(1)由图中数据可得,被抽查学生总数为:1200÷40%=3000(人),
∴该区共抽取了3000名九年级学生;
(2)90000×40%=36000(人),
∴该区九年级学生大约有36000人视力不良;
(3)有题意可得:360°×30%=108°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q.

(1)试证明:无论点P运动到AB上何处时,都有△ADQ≌△ABQ;
(2)当点P在AB上运动到什么位置时,△ADQ的面积是正方形ABCD面积的![]() ;
;
(3)若点P从点A运动到点B,再继续在BC上运动到点C,在整个运动过程中,当点P运动到什么位置时,△ADQ恰为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
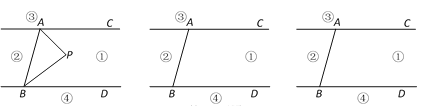
【题目】如图,直线AC∥BD,连结AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连结PA、PB,构成∠PAC、∠APB、∠PBD三个角.(提示:有公共端点的两条重合的射线所组成的角是0°)
(1)当动点P落在第①部分时,有∠APB=∠PAC+∠PBD,请说明理由;
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?若不成立,试写出∠PAC、∠APB、∠PBD三个角的等量关系(无需说明理由);
(3)当动点P在第③部分时,探究∠PAC、∠APB、∠PBD之间的关系,写出你发现的一个结论并加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】厉害了,我的国!2018年10月24日,珠港澳大桥建成通车,成了世界瞩目的焦点.这座连接中国珠海、香港、澳门三座城市,全长55公里,投资1269亿元经过6年筹备与9年建设的跨海大桥,创造了400多项专利和七项世界之最,被誉为世界的第七大奇迹,是中国科技实力的伟大展现,令全球华人倍感骄傲与自豪.用科学记数法表示大桥的投资款正确的是( )
A.12.69×![]() 亿元B.1.269×
亿元B.1.269×![]() 元
元
C.1.269×![]() 元D.1.269×
元D.1.269×![]() 元
元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点![]() 表示
表示![]() ,点
,点![]() 表示
表示![]() ,点
,点![]() 表示
表示![]() .动点
.动点![]() 从点
从点![]() 出发,沿数轴正方向以每秒
出发,沿数轴正方向以每秒![]() 个单位的速度匀速运动;同时,动点
个单位的速度匀速运动;同时,动点![]() 从点
从点![]() 出发,沿数轴负方向以每秒
出发,沿数轴负方向以每秒![]() 个单位的速度匀速运动.设运动时间为
个单位的速度匀速运动.设运动时间为![]() 秒.
秒.
(1)当![]() 为何值时,
为何值时,![]() 、
、![]() 两点相遇?相遇点
两点相遇?相遇点![]() 所对应的数是多少?
所对应的数是多少?
(2)在点![]() 出发后到达点
出发后到达点![]() 之前,求
之前,求![]() 为何值时,点
为何值时,点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到点
到点![]() 的距离相等;
的距离相等;
(3)在点![]() 向右运动的过程中,
向右运动的过程中,![]() 是
是![]() 的中点,在点
的中点,在点![]() 到达点
到达点![]() 之前,求
之前,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】广州火车南站广场计划在广场内种植A,B两种花木共 6600棵,若A花木数量是B花木数量的2倍少600棵.
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为直线AB上一点,过点O作直线OC,已知∠AOC≠90°,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE.

(1)求∠DOE和∠DOF的度数;
(2)若∠DOC=3∠COF,求∠AOC的度数;
(3)求∠BOF+∠DOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时![]() 张用A方法,其余用B方法。
张用A方法,其余用B方法。
(1)用![]() 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的轨道上有两个点甲与乙,开始时甲在A处,乙在C处,它们沿着正方形轨道顺时针同时出发,甲的速度为每秒1 cm,乙的速度为每秒5 cm,已知正方形轨道ABCD的边长为2 cm,则乙在第2 020次追上甲时的位置在( )
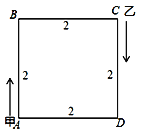
A.AB上B.BC上
C.CD上D.AD上
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com