
����Ŀ����ͼ,�ڱ߳�Ϊ4��������ABCD��,��P��AB�ϴ�A��B�˶�,����DP��AC�ڵ�Q��

��1����֤�������۵�P�˶���AB�Ϻδ�ʱ,������ADQ�ա�ABQ��
��2������P��AB���˶���ʲôλ��ʱ,��ADQ�������������ABCD�����![]() ��
��
��3������P�ӵ�A�˶�����B,�ټ�����BC���˶�����C,�������˶�������,����P�˶���ʲôλ��ʱ,��ADQǡΪ���������Σ�
���𰸡���1��֤������������2��AP=2����3��P��B�㣬C�㣬����CP=4��![]() -1��������ADQ�ǵ��������Σ�
-1��������ADQ�ǵ��������Σ�
��������
�����������1������SAS�����ADQ�ա�ABQ��
��2������Q��QE��AD��E��QF��AB��F����QE=QF������ADQ�������������ABCD�����![]() ������S��ADQ=
������S��ADQ=![]() ADQE=
ADQE=![]() S������ABCD�����OE��ֵ����������DEQ�ס�DAP��
S������ABCD�����OE��ֵ����������DEQ�ס�DAP��![]() �����APֵ��
�����APֵ��
��3����P�˶�ʱ����ADQǡΪ���������ε���������֣���QD=QA��DA=DQ��AQ=AD���������ε�����֪��������P�˶������B�غ�ʱ��QD=QA����ʱ��ADQ�ǵ��������Σ�������P���C�غ�ʱ����Q���CҲ�غϣ���ʱDA=DQ����ADQ�ǵ��������Σ�����AD=AQ=4ʱ����CP=CQ��CP=AC-AD���������εĶԽ��ߵ����ʵõ�CP��ֵ��
�����������1����������ABCD��
���۵�P�˶���AB�Ϻδ�ʱ������
AD=AB����DAQ=��BAQ��AQ=AQ��
���ADQ�ա�ABQ��
��2����ADQ�����ǡ����������ABCD�����![]() ʱ��
ʱ��
����Q��QE��AD��E��QF��AB��F����QE=QF��

���ڱ߳�Ϊ4��������ABCD�У�
��S������ABCD=16��
��![]() AD��QE=
AD��QE=![]() S������ABCD=
S������ABCD=![]() ��16=
��16=![]() ��
��
��QE=![]() ��
��
��EQ��AP��
���DEQ�ס�DAP��
��![]() ����
����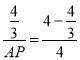 ��
��
���AP=2��
��AP=2ʱ����ADQ�������������ABCD�����![]() ��
��
��3������ADQ�ǵ��������Σ�����QD=QA��DA=DQ��AQ=AD��
����AD=DQʱ������DQA=��DAQ=45��
���ADQ=90����PΪC�㣬
����AQ=DQʱ������DAQ=��ADQ=45����
���AQD=90����PΪB��
��AD=AQ��P��BC�ϣ���
��CQ=AC-AQ=![]() BC-BC=��
BC-BC=��![]() -1��BC
-1��BC
��AD��BC
��![]() �����ɵ�
�����ɵ�![]() =1��
=1��
��CP=CQ=��![]() -1��BC=4��
-1��BC=4��![]() -1��
-1��
���ϣ�P��B�㣬C�㣬����CP=4��![]() -1��������ADQ�ǵ��������Σ�
-1��������ADQ�ǵ��������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�й涨ÿ����ˮ18�����ڣ�����18�֣����û���ÿ����ˮ��aԪ��һ������ˮ����18�ֵ��û���18��ˮ��ÿ��aԪ�շѣ�����18�ֵIJ��֣���ÿ��bԪ��ba���շ�.��һ������ÿ����ˮx�֣�Ӧ��ˮ��yԪ��y��x֮��ĺ�����ϵ��ͼ��
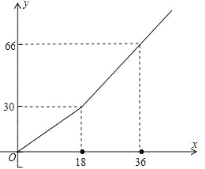
��1����a��ֵ��ij������������ˮ10�֣�Ӧ��ˮ�Ѷ���Ԫ��
��2����b��ֵ����д����x18ʱ��y��x֮��ĺ�����ϵʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ٰ�У�Ļ������ڣ��ס������������ϳ�ͬѧ�����ݳ���װ(һ��һ��)�����92��(���мװ���Ұ��˶࣬�Ҽװ��90��)�������ǹ����̸������ݳ���װ�ļ۸����
�����װ������ | 1����45�� | 46����90�� | 91������ |
ÿ��װ�ļ۸� | 60Ԫ | 50Ԫ | 40Ԫ |
����������ÿλͬѧ����һ��װ����ôһ��Ӧ��5020Ԫ��
(1)�ס�����������������ÿλͬѧ����һ��װ���ȵ���������Խ�ʡ����Ǯ��
(2)�ס���������ж�����ͬѧ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�ĶԽ����ཻ�ڵ�O����AD��AB������O��OE��AC��AD�ڵ�E������CE����ƽ���ı���ABCD���ܳ�Ϊ20�����CDE���ܳ��ǣ�������
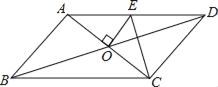
A. 10B. 11C. 12D. 13
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��8��0�����ڵ�һ���Ķ���P��x��y������x+y=10������OPA�����ΪS
��1����S����x�ĺ�������ʽ��
��2����x��ȡֵ��Χ��
��3����S=12ʱP�����ꣻ
��4����������S��ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪������y=x2+bx+c����A��B��C���㣬��֪B��4��0����C��2����6����
��1����������ߵĽ���ʽ�͵�A�����ꣻ
��2����D��m��n������1��m��2����������ͼ���ϣ�����ACD�����Ϊ![]() ʱ�����D�����ꣻ
ʱ�����D�����ꣻ
��3���ڣ�2���������£��������ߵĶԳ���Ϊl����D����l�ĶԳƵ�ΪE���ܷ���������ͼ���l�Ϸֱ��ҵ���P��Q��ʹ���Ե�D��E��P��QΪ������ı���Ϊƽ���ı��Σ����ܣ������P�����ꣻ�����ܣ���˵�����ɣ�
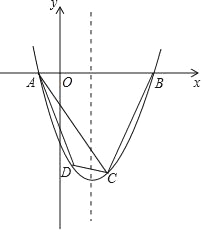
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABC�У���BAC��90������DΪBC���е㣬��E��AC�ϣ�����CDE��DE�۵���ʹ�õ�Cǡ������BA���ӳ����ϵĵ�F��������AD�������н��۲�һ����ȷ���ǣ�������

A. AE=EF B. AB=2DE
C. ��ADF����ADE�������� D. ��ADE����FDE��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��ڽ���ƽ��ֱ������ϵ����ABC�Ķ�����ڸ���ϣ���B������Ϊ��1��0��
��1��������ABC����x��ԳƵ���A1B1C1��
��2����������ABC��ԭ��O����ʱ����ת90�����õ���A2B2C2��
��3����A1B1C1����A2B2C2����Գ�ͼ����������Գ�ͼ�Σ��������еĶԳ��
��4����A1B1C1����A2B2C2�����ĶԳ�ͼ�����������ĶԳ�ͼ�Σ�д�����еĶԳ����ĵ����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��Ϊ����ѧ���������仯���,��ȫ�����꼶ѧ���г�ȡ�˲���ѧ��,ͳ����ÿ�������������������Ľ��,�����������ݴ�����,�Ƴ�����ͳ��ͼ������ͳ��ͼ����:
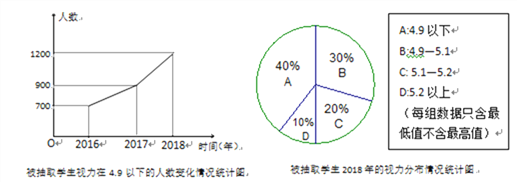
�����������:
��1����������ȡ�˶��������꼶ѧ��?
��2������������9�������꼶ѧ��,�������2018���������������4.9���£��ĸ��꼶ѧ�����ж�����?
��3������ͳ��ͼ��B��Բ�ĽǶ���Ϊ____.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com