练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某市规定每月用水18吨以内（包括18吨）的用户，每吨收水费a元：一个月用水超过18吨的用户，18吨水仍按每吨a元收费，超过18吨的部分，按每吨b元（ba）收费.设一户居民每月用水x吨，应收水费y元，y与x之间的函数关系如图；

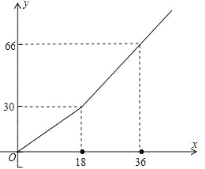
    （1）求a的值，某户居民上月用水10吨，应收水费多少元；

    （2）求b的值，并写出当x18时，y与x之间的函数关系式.

    【答案】（1），用水10吨应收水费元；（2）b=2，当x18时，y=2x－6.

    【解析】

    （1）分析图象可知，用水18吨交了30元，由此求出a的值即可；

    （2）由图象可知，x18时，可设y与x之间的函数关系式为，再把x=36，y=66代入，即可解决问题.

    解：（1）由图象知，用水18吨交了30元，所以，

    用水10吨应收水费元；

    （2）由图象可知，x18时，设y与x之间的函数关系式为，

    把x=36，y=66代入，得66=b×(36－18)+30，解得b=2，

    ∴y与x之间的函数关系式为y=2（x－18）+30=2x－6.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图①所示，在直角梯形ABCD中，∠BAD=90°，E是直线AB上一点，过E作直线l∥BC，交直线CD于点F．将直线l向右平移，设平移距离BE为t（t≥0），直角梯形ABCD被直线l扫过的面积（图中阴影部分）为S，S关于t的函数图象如图②所示，OM为线段，MN为抛物线的一部分，NQ为射线，N点横坐标为4．

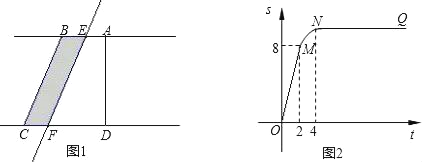
    信息读取

    （1）梯形上底的长AB=　 　；

    （2）直角梯形ABCD的面积=　 　；

    图象理解

    （3）写出图②中射线NQ表示的实际意义；

    （4）当2＜t＜4时，求S关于t的函数关系式；

    问题解决

    （5）当t为何值时，直线l将直角梯形ABCD分成的两部分面积之比为1：3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在矩形ABCD中,AD=3，CD=4,点E在边CD上,且DE=1.

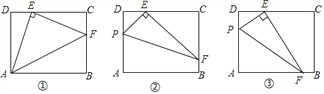
    （1）感知：如图①，连接AE，过点E作，交BC于点F，连接AF，易证： (不需要证明)；

    （2）探究：如图②，点P在矩形ABCD的边AD上(点P不与点A、D重合)，连接PE，过点E ,交BC于点F，连接PF.求证： 相似;

    （3）应用：如图③，若EF交AB边于点F， ，其他条件不变，且的面积是6，则AP的长为____.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知在纸面上有一数轴（如图），折叠纸面.

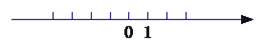
    （1）若1表示的点与－1表示的点重合，则－2表示的点与数 表示的点重合；

    （2）若－1表示的点与3表示的点重合，回答以下问题：

    ① 5表示的点与数 表示的点重合；

    ② 若数轴上A、B两点之间的距离为9（A在B的左侧），且A、B两点经折叠后重合，求A、B两点表示的数是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下表是今年某水库一周内的水位变化情况(正号表示水位比前一天上升，负号表示水位比前一天下降)，该水库的警戒水位是. (上周末的水位达到警戒水位).

    星期

    一

    二

    三

    四

    五

    六

    日

    水位变化/

    (1)本周星期________河流的水位最高，水位是________，本周星期________河流的水位最低，水位是________；

    (2)本周三的水位位于警戒水位之_____(填“上”或“下”)，与警戒水位的距离是______；

    (3)与上周末相比，本周末河流水位是上升了还是下降了？变化了多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

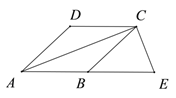
    【题目】如图，在菱形ABCD中，CE垂直对角线AC于点C，AB的延长线交CE于点E.

    （1）求证：CD＝BE；

    （2）如果∠E＝60°，CE=m，请写出求菱形ABCD面积的思路．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

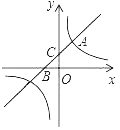
    【题目】如图，直线y＝x+b与双曲线y＝（k为常数，k≠0）在第一象限内交于点A（1，2），且与x轴、y轴分别交于B，C两点．

    （1）求直线和双曲线的解析式；

    （2）点P在x轴上，且△BCP的面积等于2，求P点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，A(1，2)，B(3，1)，C(-2，-1).

    （1）在图中作出关于轴对称的.

    （2）写出点的坐标（直接写答案）.

    A1_____________，B1______________，C1______________

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连接DP交AC于点Q．

    （1）试证明：无论点P运动到AB上何处时,都有△ADQ≌△ABQ；

    （2）当点P在AB上运动到什么位置时,△ADQ的面积是正方形ABCD面积的；

    （3）若点P从点A运动到点B,再继续在BC上运动到点C,在整个运动过程中,当点P运动到什么位置时,△ADQ恰为等腰三角形．

    查看答案和解析>>

    同步练习册答案