
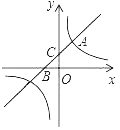
【题目】如图,直线y=x+b与双曲线y=![]() (k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
(k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
(1)求直线和双曲线的解析式;
(2)点P在x轴上,且△BCP的面积等于2,求P点的坐标.
【答案】(1)y=![]() ;y=x+1;(2)P点的坐标为(3,0)或(﹣5,0).
;y=x+1;(2)P点的坐标为(3,0)或(﹣5,0).
【解析】
(1)把A(1,2)代入双曲线以及直线y=x+b,分别可得k,b的值;
(2)先根据直线解析式得到BO=CO=1,再根据△BCP的面积等于2,即可得到P的坐标.
解:(1)把A(1,2)代入双曲线y=![]() ,可得k=2,
,可得k=2,
∴双曲线的解析式为y=![]() ;
;
把A(1,2)代入直线y=x+b,可得b=1,
∴直线的解析式为y=x+1;
(2)设P点的坐标为(x,0),
在y=x+1中,令y=0,则x=﹣1;令x=0,则y=1,
∴B(﹣1,0),C(0,1),即BO=1=CO,
∵△BCP的面积等于2,
∴![]() BP×CO=2,即
BP×CO=2,即![]() |x﹣(﹣1)|×1=2,
|x﹣(﹣1)|×1=2,
解得x=3或﹣5,
∴P点的坐标为(3,0)或(﹣5,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
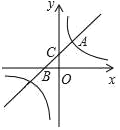
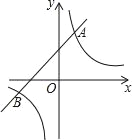
【题目】已知一次函数y1=kx+b(k≠0)与反比例函数y2=![]() (m≠0)相交于A和B两点,且A点坐标为(1,3),B点的横坐标为﹣3.
(m≠0)相交于A和B两点,且A点坐标为(1,3),B点的横坐标为﹣3.
(1)求反比例函数和一次函数的解析式;
(2)根据图象直接写出使得y1>y2时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校2019学年举行席地绘画大赛.共收到绘画作品480件,其中的优秀作品评出了一、二、三等奖.
占获奖总数的几分之几 | 获奖作品的件数 | |
一等奖 |
| b |
二等奖 |
| c |
三等奖 | a | 96 |
(1)则a= ;b= ;c= ;
(2)学校决定为获一等奖同学每人购买一个书包,获得二等奖同学每人购买一个文具盒,获得三等奖同学每人购买一支钢笔,并且每位获奖同学颁发一个证书,已知文具盒单价是书包单价的![]() ,证书的单价是文具盒单价的
,证书的单价是文具盒单价的![]() ,钢笔的单介是文具盒单价的
,钢笔的单介是文具盒单价的![]() ,学校购买书包、文具盒、钢笔共用4000元,那么学校购买证书共用了多少元?
,学校购买书包、文具盒、钢笔共用4000元,那么学校购买证书共用了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市规定每月用水18吨以内(包括18吨)的用户,每吨收水费a元:一个月用水超过18吨的用户,18吨水仍按每吨a元收费,超过18吨的部分,按每吨b元(ba)收费.设一户居民每月用水x吨,应收水费y元,y与x之间的函数关系如图;
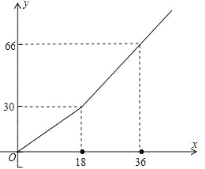
(1)求a的值,某户居民上月用水10吨,应收水费多少元;
(2)求b的值,并写出当x18时,y与x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织同学到离校15千米的社会实践基地开展活动.一部分同学骑自行车前往,另一部分同学在骑自行车的同学出发![]() 小时后,乘汽车沿相同路线行进,结果骑自行车的与乘汽车的同学同时到达目的地.已知汽车速度是自行车速度的3倍,求自行车的速度.
小时后,乘汽车沿相同路线行进,结果骑自行车的与乘汽车的同学同时到达目的地.已知汽车速度是自行车速度的3倍,求自行车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.
利用数形结合思想回答下列问题:
(1)数轴上表示1和3两点之间的距离 .
(2)数轴上表示﹣12和﹣6的两点之间的距离是 .
(3)数轴上表示x和1的两点之间的距离表示为 .
(4)若x表示一个有理数,且﹣4<x<2,则|x﹣2|+|x+4|= .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“元旦”期间,某文具店购进 ![]() 只两种型号的文具进行销售,其进价和售价如表:
只两种型号的文具进行销售,其进价和售价如表:
型号 | 进价(元/只) | 售价(元/只) |
A型 | 10 | 12 |
B型 | 15 | 23 |
(1)该店用 ![]() 元可以购进A,B两种型号的文具各多少只?
元可以购进A,B两种型号的文具各多少只?
(2)在(![]() )的条件下,若把所购进A,B两种型号的文具全部销售完,利润率有没有超过
)的条件下,若把所购进A,B两种型号的文具全部销售完,利润率有没有超过 ![]() ?请你说明理由.
?请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为举办校园文化艺术节,甲、乙两班准备给合唱同学购买演出服装(一人一套),两班共92人(其中甲班比乙班人多,且甲班不到90人),下面是供货商给出的演出服装的价格表:
购买服装的套数 | 1套至45套 | 46套至90套 | 91套以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
如果两班单独给每位同学购买一套服装,那么一共应付5020元.
(1)甲、乙两班联合起来给每位同学购买一套服装,比单独购买可以节省多少钱?
(2)甲、乙两班各有多少名同学?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠BAC>90°,点D为BC的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连结AD,则下列结论不一定正确的是( )

A. AE=EF B. AB=2DE
C. △ADF和△ADE的面积相等 D. △ADE和△FDE的面积相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com