
【题目】某学校2019学年举行席地绘画大赛.共收到绘画作品480件,其中的优秀作品评出了一、二、三等奖.
占获奖总数的几分之几 | 获奖作品的件数 | |
一等奖 |
| b |
二等奖 |
| c |
三等奖 | a | 96 |
(1)则a= ;b= ;c= ;
(2)学校决定为获一等奖同学每人购买一个书包,获得二等奖同学每人购买一个文具盒,获得三等奖同学每人购买一支钢笔,并且每位获奖同学颁发一个证书,已知文具盒单价是书包单价的![]() ,证书的单价是文具盒单价的
,证书的单价是文具盒单价的![]() ,钢笔的单介是文具盒单价的
,钢笔的单介是文具盒单价的![]() ,学校购买书包、文具盒、钢笔共用4000元,那么学校购买证书共用了多少元?
,学校购买书包、文具盒、钢笔共用4000元,那么学校购买证书共用了多少元?
【答案】(1)![]() ,b=32,c=64;(2)共用576元
,b=32,c=64;(2)共用576元
【解析】
(1)根据所给信息,计算一、二等奖占获奖总数的多少即可求出a,再根据题意列方程、再解方程即可求出b和c的值;
(2)设文具盒的单价为x元,然后表示出其他物品的单价,最后列出一元一次方程求解即可.
解:(1)![]()
设获奖作品的件数为x件.
根据题意,得![]() x=b,
x=b,![]() x=c,ax=96,
x=c,ax=96,
解得:b=32,c=64
故答案为![]() 、32、64.
、32、64.
()设文具盒的单价为x元,则钢笔的单价为![]() x元,书包的单价为x÷
x元,书包的单价为x÷![]() =
=![]() x元,证书的
x元,证书的
价为![]() x元.根据题意,得
x元.根据题意,得
32×![]() x +64x+96×
x +64x+96×![]() x=4000
x=4000
解得x=30
则证书共用了192×![]() x=192×
x=192×![]() ×30=576.
×30=576.
答:学年购买证书共用576元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
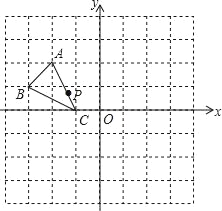
【题目】如图,在8×8的方格中建立平面直角坐标系,有点A(﹣2,2)、B(﹣3,1)、C(﹣1,0),P(a,b)是△ABC的AC边上点,将△ABC平移后得到△A1B1C1,点P的对应点为P1(a+4,b+2).
(1)画出平移后的△A1B1C1,写出点A1、C1的坐标;
(2)若以A、B、C、D为顶点的四边形为平行四边形,写出方格中D点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y= ![]() x+6分别与x轴、y轴交于A、B两点:直线y=
x+6分别与x轴、y轴交于A、B两点:直线y= ![]() x与AB于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的进度沿x轴向左运动.过点E作x轴的垂线,分別交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠的图形的周长为L个单位长度,点E的运动时间为t(秒).
x与AB于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的进度沿x轴向左运动.过点E作x轴的垂线,分別交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠的图形的周长为L个单位长度,点E的运动时间为t(秒).
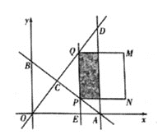
(1)直接写出点C和点A的坐标.
(2)若四边形OBQP为平行四边形,求t的值.
(3)0<t<5时,求L与t之间的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AD=3,CD=4,点E在边CD上,且DE=1.
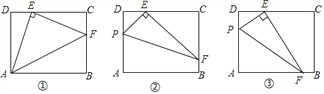
(1)感知:如图①,连接AE,过点E作![]() ,交BC于点F,连接AF,易证:
,交BC于点F,连接AF,易证: ![]() (不需要证明);
(不需要证明);
(2)探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E ![]() ,交BC于点F,连接PF.求证:
,交BC于点F,连接PF.求证: ![]() 相似;
相似;
(3)应用:如图③,若EF交AB边于点F, ![]() ,其他条件不变,且
,其他条件不变,且![]() 的面积是6,则AP的长为____.
的面积是6,则AP的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
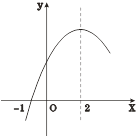
【题目】二次函数![]() 的部分图象如图③所示,图象过点(-1,0),对称轴为直线
的部分图象如图③所示,图象过点(-1,0),对称轴为直线![]() =2,则下列结论中正确的个数有( )
=2,则下列结论中正确的个数有( )
①4![]() +b=0;②
+b=0;②![]() ;③若点A(-3,
;③若点A(-3, ![]() ),点B(-
),点B(-![]() ,
, ![]() ),点C(5,
),点C(5, ![]() )在该函数图象上,则
)在该函数图象上,则![]() <
<![]() <
<![]() ;④若方程
;④若方程![]() 的两根为
的两根为![]() 和
和![]() ,且
,且![]() <
<![]() ,则
,则![]() <-1<5<
<-1<5<![]() .
.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在纸面上有一数轴(如图),折叠纸面.
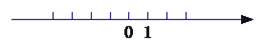
(1)若1表示的点与-1表示的点重合,则-2表示的点与数 表示的点重合;
(2)若-1表示的点与3表示的点重合,回答以下问题:
① 5表示的点与数 表示的点重合;
② 若数轴上A、B两点之间的距离为9(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是今年某水库一周内的水位变化情况(正号表示水位比前一天上升,负号表示水位比前一天下降),该水库的警戒水位是![]() . (上周末的水位达到警戒水位).
. (上周末的水位达到警戒水位).
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化/ |
|
|
|
|
|
|
|
(1)本周星期________河流的水位最高,水位是________![]() ,本周星期________河流的水位最低,水位是________
,本周星期________河流的水位最低,水位是________![]() ;
;
(2)本周三的水位位于警戒水位之_____(填“上”或“下”),与警戒水位的距离是______![]() ;
;
(3)与上周末相比,本周末河流水位是上升了还是下降了?变化了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
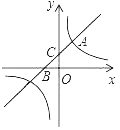
【题目】如图,直线y=x+b与双曲线y=![]() (k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
(k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
(1)求直线和双曲线的解析式;
(2)点P在x轴上,且△BCP的面积等于2,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
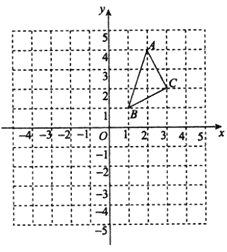
【题目】△ABC在平面直角坐标系中的位置如图所示,A,B,C三点在格点上.
(1)作出△ABC关于x轴对称的△A1B1C1,并写出点A1、B1、C1的坐标;
(2)作出△ABC关于原点O对称的△A2B2C2,并写出点A2、B2、C2的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com