
【题目】如图,直线y= ![]() x+6分别与x轴、y轴交于A、B两点:直线y=
x+6分别与x轴、y轴交于A、B两点:直线y= ![]() x与AB于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的进度沿x轴向左运动.过点E作x轴的垂线,分別交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠的图形的周长为L个单位长度,点E的运动时间为t(秒).
x与AB于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的进度沿x轴向左运动.过点E作x轴的垂线,分別交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠的图形的周长为L个单位长度,点E的运动时间为t(秒).
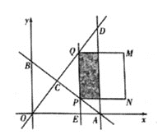
(1)直接写出点C和点A的坐标.
(2)若四边形OBQP为平行四边形,求t的值.
(3)0<t<5时,求L与t之间的函数解析式.
【答案】(1)![]() ,
,![]() ;(2)2;(3)
;(2)2;(3)![]() .
.
【解析】
(1)把y= ![]() x+6和 y=
x+6和 y= ![]() x联立组成方程组,解方程组求得方程组的解,即可得点C的坐标;在直线y=
x联立组成方程组,解方程组求得方程组的解,即可得点C的坐标;在直线y= ![]() x+6中,令y=0,求得x的值,即可得点A的坐标;(2)用t表示出点P、Q的坐标,求得PQ的长,由条件可知,BO∥QP,若使四边形OBQP为平行四边形,必须满足OB=QP,由此可得
x+6中,令y=0,求得x的值,即可得点A的坐标;(2)用t表示出点P、Q的坐标,求得PQ的长,由条件可知,BO∥QP,若使四边形OBQP为平行四边形,必须满足OB=QP,由此可得![]() ,即可求得t值;(3)由题意可知,正方形PQMN与△ACD重叠的图形是矩形,由此求得L与t之间的函数解析式即可.
,即可求得t值;(3)由题意可知,正方形PQMN与△ACD重叠的图形是矩形,由此求得L与t之间的函数解析式即可.
(1)C的坐标为( ![]() ),A的坐标为(8,0);
),A的坐标为(8,0);
(2)∵点B直线y= ![]() x+6与y轴的交点,
x+6与y轴的交点,
∴B(0,6),
∴OB=6,
∵A的坐标为(8,0),
∴OA=8,
由题意可得,OE=8-t,
∴P(8-t,![]() ),Q(8-t,
),Q(8-t,![]() )
)
∴![]() =10-2t,
=10-2t,
由条件可知,BO∥QP,若使四边形OBQP为平行四边形,必须满足OB=QP,
所以有 ![]() ,解得t=2;
,解得t=2;
(3)当0<t<5时, ![]() .
.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源: 题型:
【题目】如果一元二次方程ax2+bx+c=0(a≠0)满足4a-2b+c=0,且有两个相等的实数根,则( )
A. b=aB. c=2aC. a(x+2)2=0(a≠0)D. a(x-2)2=0(a≠0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面解方程![]() 的步骤,在后面的横线上填写此步骤的依据:
的步骤,在后面的横线上填写此步骤的依据:
解:去分母,得![]() .①依据:_________
.①依据:_________
去括号,得![]() .
.
移项,得![]() .②依据:__________
.②依据:__________
合并同类项,得![]() .
.
系数化为1,得![]() .
.
∴![]() 是原方程的解.
是原方程的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
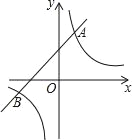
【题目】已知一次函数y1=kx+b(k≠0)与反比例函数y2=![]() (m≠0)相交于A和B两点,且A点坐标为(1,3),B点的横坐标为﹣3.
(m≠0)相交于A和B两点,且A点坐标为(1,3),B点的横坐标为﹣3.
(1)求反比例函数和一次函数的解析式;
(2)根据图象直接写出使得y1>y2时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“端午”期间,小明、小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
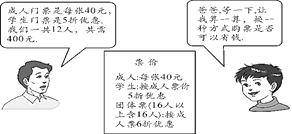
(1)他们共去了几个成人,几个学生?
(2)请你帮助算算,小明用更省钱的购票方式是指什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲沿周长为300米的环形跑道上按逆时针方向跑步,速度为a米/秒,与此同时在甲后面100米的乙也沿该环形跑道按逆时针方向跑步,速度为3米/秒.设运动时间为t秒.
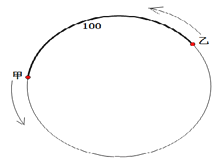
(1)若a=5,求甲、乙两人第1次相遇的时间;
(2)当t=50时,甲、乙两人第1次相遇.
①求a的值;
②若![]() 时,甲、乙两人第1次相遇前,当两人相距120米时,求
时,甲、乙两人第1次相遇前,当两人相距120米时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() 的图象与直线y=﹣x+b都经过点A(1,4),且该直线与x轴的交点为B.
的图象与直线y=﹣x+b都经过点A(1,4),且该直线与x轴的交点为B.
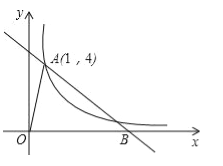
(1)求反比例函数和直线的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校2019学年举行席地绘画大赛.共收到绘画作品480件,其中的优秀作品评出了一、二、三等奖.
占获奖总数的几分之几 | 获奖作品的件数 | |
一等奖 |
| b |
二等奖 |
| c |
三等奖 | a | 96 |
(1)则a= ;b= ;c= ;
(2)学校决定为获一等奖同学每人购买一个书包,获得二等奖同学每人购买一个文具盒,获得三等奖同学每人购买一支钢笔,并且每位获奖同学颁发一个证书,已知文具盒单价是书包单价的![]() ,证书的单价是文具盒单价的
,证书的单价是文具盒单价的![]() ,钢笔的单介是文具盒单价的
,钢笔的单介是文具盒单价的![]() ,学校购买书包、文具盒、钢笔共用4000元,那么学校购买证书共用了多少元?
,学校购买书包、文具盒、钢笔共用4000元,那么学校购买证书共用了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“元旦”期间,某文具店购进 ![]() 只两种型号的文具进行销售,其进价和售价如表:
只两种型号的文具进行销售,其进价和售价如表:
型号 | 进价(元/只) | 售价(元/只) |
A型 | 10 | 12 |
B型 | 15 | 23 |
(1)该店用 ![]() 元可以购进A,B两种型号的文具各多少只?
元可以购进A,B两种型号的文具各多少只?
(2)在(![]() )的条件下,若把所购进A,B两种型号的文具全部销售完,利润率有没有超过
)的条件下,若把所购进A,B两种型号的文具全部销售完,利润率有没有超过 ![]() ?请你说明理由.
?请你说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com