
【题目】二次函数![]() 的部分图象如图③所示,图象过点(-1,0),对称轴为直线
的部分图象如图③所示,图象过点(-1,0),对称轴为直线![]() =2,则下列结论中正确的个数有( )
=2,则下列结论中正确的个数有( )
①4![]() +b=0;②
+b=0;②![]() ;③若点A(-3,
;③若点A(-3, ![]() ),点B(-
),点B(-![]() ,
, ![]() ),点C(5,
),点C(5, ![]() )在该函数图象上,则
)在该函数图象上,则![]() <
<![]() <
<![]() ;④若方程
;④若方程![]() 的两根为
的两根为![]() 和
和![]() ,且
,且![]() <
<![]() ,则
,则![]() <-1<5<
<-1<5<![]() .
.
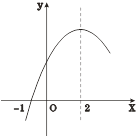
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】试题解析:由抛物线的对称轴为x=2可得-![]() =2,即4a+b=0,故①正确;
=2,即4a+b=0,故①正确;
由抛物线的对称性知x=0和x=4时,y>0,
则x=3时,y=9a+3b+c>0,故②错误;
∵抛物线的开口向下,且对称轴为x=2,
∴抛物线上离对称轴水平距离越小,函数值越大,
∵点A到x=2的水平距离为5,点B到对称轴的水平距离为2.5,点C到对称轴的水平距离为3,
∴y1<y3<y2,故③正确;
令y=a(x+1)(x-5),
则抛物线y=a(x+1)(x-5)与y=ax2+bx+c形状相同、开口方向相同,且与x轴的交点为(-1,0)、(3,0),
函数图象如图所示,
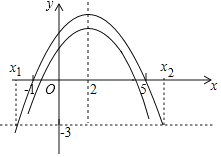
由函数图象可知方程a(x+1)(x-5)=-3的两根即为抛物线y=a(x+1)(x-5)与直线y=-3交点的横坐标,
∴x1<-1<5<x2,故④正确;
故选C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
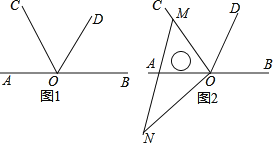
【题目】如图1,点O为直线AB上一点,过点O作射线OC,OD,使射线OC平分∠AOD.
(1)当∠BOD=50°时,∠COD= °;
(2)将一直角三角板的直角顶点放在点O处,当三角板MON的一边OM与射线OC重合时,如图2.
①在(1)的条件下,∠AON= °;
②若∠BOD=70°,求∠AON的度数;
③若∠BOD=α,请直接写出∠AON的度数(用含α的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“端午”期间,小明、小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
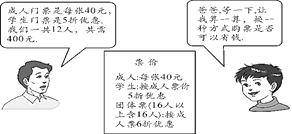
(1)他们共去了几个成人,几个学生?
(2)请你帮助算算,小明用更省钱的购票方式是指什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() 的图象与直线y=﹣x+b都经过点A(1,4),且该直线与x轴的交点为B.
的图象与直线y=﹣x+b都经过点A(1,4),且该直线与x轴的交点为B.
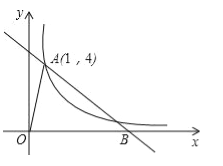
(1)求反比例函数和直线的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
按照一定顺序排列着的一列数称为数列,数列中的每一个数叫做这个数列的项.排在第一位的数称为第一项,记为a1,排在第二位的数称为第二项,记为a2,以此类推,排在第n位的数称为第n项,记为![]() .所以,数列的一般形式可以写成:
.所以,数列的一般形式可以写成:![]() ,…,
,…,![]() ,…,一般的,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,那么这个数列叫做等差数列,这个常数叫做等差数列公差,公差通常用d表示.如:数列1,3,5,7,…为等差数列,期中a1=1,a2=3,公差为d=2.根据以上材料,解答下列问题:
,…,一般的,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,那么这个数列叫做等差数列,这个常数叫做等差数列公差,公差通常用d表示.如:数列1,3,5,7,…为等差数列,期中a1=1,a2=3,公差为d=2.根据以上材料,解答下列问题:
(1)等差数列5,10,15,…的公差d为 ,第5项是 .
(2)如果一个数列![]() ,…,
,…,![]() ,…,是等差数列,且公差为d,那么根据定义可得到:
,…,是等差数列,且公差为d,那么根据定义可得到:![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,….所以
,….所以
![]()
![]()
![]()
……由此,请你填空完成等差数列的通项公式:![]() ( )d
( )d
(3)求-4039是等差数列-5,-7,-9,…的第几项?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校2019学年举行席地绘画大赛.共收到绘画作品480件,其中的优秀作品评出了一、二、三等奖.
占获奖总数的几分之几 | 获奖作品的件数 | |
一等奖 |
| b |
二等奖 |
| c |
三等奖 | a | 96 |
(1)则a= ;b= ;c= ;
(2)学校决定为获一等奖同学每人购买一个书包,获得二等奖同学每人购买一个文具盒,获得三等奖同学每人购买一支钢笔,并且每位获奖同学颁发一个证书,已知文具盒单价是书包单价的![]() ,证书的单价是文具盒单价的
,证书的单价是文具盒单价的![]() ,钢笔的单介是文具盒单价的
,钢笔的单介是文具盒单价的![]() ,学校购买书包、文具盒、钢笔共用4000元,那么学校购买证书共用了多少元?
,学校购买书包、文具盒、钢笔共用4000元,那么学校购买证书共用了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1是由大小相同的小立方块搭成的几何体,请在图2的方格中画出从上面和左面看到的该几何体的形状图.(只需用2B铅笔将虚线化为实线)
(2)若要用大小相同的小立方块搭一个几何体,使得它从上面和左面看到的形状图与你在图2方格中所画的形状图相同,则搭这样的一个几何体最多需要 个小立方块.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织同学到离校15千米的社会实践基地开展活动.一部分同学骑自行车前往,另一部分同学在骑自行车的同学出发![]() 小时后,乘汽车沿相同路线行进,结果骑自行车的与乘汽车的同学同时到达目的地.已知汽车速度是自行车速度的3倍,求自行车的速度.
小时后,乘汽车沿相同路线行进,结果骑自行车的与乘汽车的同学同时到达目的地.已知汽车速度是自行车速度的3倍,求自行车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A的坐标为(0,m),且m≠0,点B的坐标为(n,0),将线段AB绕点B旋转90°,分别得到线段B P1,B P2,称点P1,P2为点A关于点B的“伴随点”,图1为点A关于点B的“伴随点”的示意图.
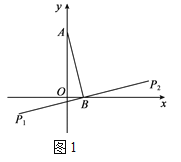
(1)已知点A(0,4),
①当点B的坐标分别为(1,0),(-2,0)时,点A关于点B的“伴随点”的坐标分别为 ;
②点(x,y)是点A关于点B的“伴随点”,直接写出y与x之间的关系式;
(2)如图2,点C的坐标为(-3,0),以C为圆心, ![]() 为半径作圆,若在⊙C上存在点A关于点B的“伴随点”,直接写出点A的纵坐标m的取值范围.
为半径作圆,若在⊙C上存在点A关于点B的“伴随点”,直接写出点A的纵坐标m的取值范围.
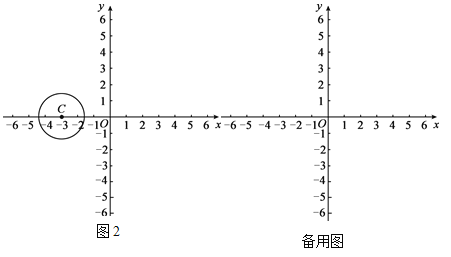
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com