
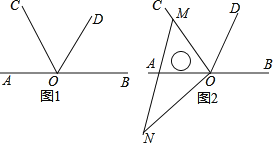
【题目】如图1,点O为直线AB上一点,过点O作射线OC,OD,使射线OC平分∠AOD.
(1)当∠BOD=50°时,∠COD= °;
(2)将一直角三角板的直角顶点放在点O处,当三角板MON的一边OM与射线OC重合时,如图2.
①在(1)的条件下,∠AON= °;
②若∠BOD=70°,求∠AON的度数;
③若∠BOD=α,请直接写出∠AON的度数(用含α的式子表示).
【答案】(1)65°;(2)①25°;②35°;③![]()
【解析】
(1)由题意可得![]() COD=
COD=![]() ,
,![]() AOD=
AOD=![]() AOB-
AOB-![]() BOD.
BOD.
(2)①由(1)可得∠AOC=∠COD=65°,∠AON=90°﹣∠AOC=25°
②同①可得,∠AOC=∠COD=55°,∠AON=90°﹣∠AOC=35°
③根据(2)可直接得出结论.
解:(1)∠AOD=180°﹣∠BOD=130°,
∵OC平分∠AOD,
∴∠COD=![]() =65°.
=65°.
故答案为:65°;
(2)①由(1)可得∠AOC=∠COD=65°,
∴∠AON=90°﹣∠AOC=25°,
故答案为:25°;
②∵∠BOD=70°,
∴∠AOD=180°﹣∠BOD=110°,
∵OC平分∠AOD,
∴∠AOC=![]() ,
,
∵∠MON=90°,
∴∠AON=90°﹣∠AOC=35°;
③ ![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,∠BAD的平分线与BC的延长线交于点E、与DC交于点F,且点F为边DC的中点,∠ADC的平分线交AB于点M,交AE于点N,连接DE
(1) 求证:BC=CE
(2) 若DM=2,求DE的长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块直角三角形的绿地,量得两直角边长分别为6m和8m,现在要将绿地扩充成等腰三角形,且扩充部分是以8m为直角边的直角三角形,求扩充后等腰三角形绿地的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
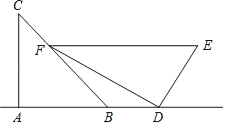
【题目】小敏是一位善于思考的学生,在一次数学活动课上,她将一副三角板按如图位置摆放,A、B、D在同一直线上,EF∥AD,∠BAC=∠EDF=90°,∠C=45°,∠E=60°,测得DE=8,则BD的长是( )
A. 10+4![]() B. 10﹣4
B. 10﹣4![]() C. 12﹣4
C. 12﹣4![]() D. 12+4
D. 12+4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
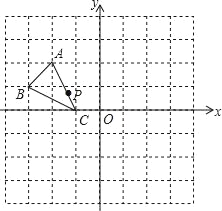
【题目】如图,在8×8的方格中建立平面直角坐标系,有点A(﹣2,2)、B(﹣3,1)、C(﹣1,0),P(a,b)是△ABC的AC边上点,将△ABC平移后得到△A1B1C1,点P的对应点为P1(a+4,b+2).
(1)画出平移后的△A1B1C1,写出点A1、C1的坐标;
(2)若以A、B、C、D为顶点的四边形为平行四边形,写出方格中D点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
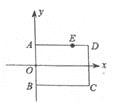
【题目】如图,已知矩形ABCD,AB在y轴上,AB=2,BC=3,点A的坐标为(0,1),在AD边上有一点E(2,1),过点E的直线与BC交于点F.若EF平分矩形ABCD的面积,则直线EF的解析式为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长均为1的小正方形网格纸中,△OAB的顶点O,A,B均在格点上,且O是直角坐标系的原点,点A在![]() 轴上.
轴上.
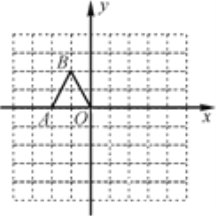
(1)以O为位似中心,将△OAB放大,使得放大后的△OA1B1与△OAB对应线段的比为2∶1,画出△OA1B1
(所画△OA1B1与△OAB在原点两侧);
(2)直接写出点A1、B1的坐标______________________.
(3)直接写出![]() ____________.
____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
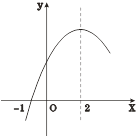
【题目】二次函数![]() 的部分图象如图③所示,图象过点(-1,0),对称轴为直线
的部分图象如图③所示,图象过点(-1,0),对称轴为直线![]() =2,则下列结论中正确的个数有( )
=2,则下列结论中正确的个数有( )
①4![]() +b=0;②
+b=0;②![]() ;③若点A(-3,
;③若点A(-3, ![]() ),点B(-
),点B(-![]() ,
, ![]() ),点C(5,
),点C(5, ![]() )在该函数图象上,则
)在该函数图象上,则![]() <
<![]() <
<![]() ;④若方程
;④若方程![]() 的两根为
的两根为![]() 和
和![]() ,且
,且![]() <
<![]() ,则
,则![]() <-1<5<
<-1<5<![]() .
.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com