
【题目】如图,在平行四边形ABCD中,AB=6,∠BAD的平分线与BC的延长线交于点E、与DC交于点F,且点F为边DC的中点,∠ADC的平分线交AB于点M,交AE于点N,连接DE
(1) 求证:BC=CE
(2) 若DM=2,求DE的长

【答案】(1)证明见解析;(2)DE=![]() .
.
【解析】
(1)利用平行四边形ABCD的性质得出AD=BC,AD∥BC,进一步证得△ADF≌△ECF,得出AD=CE,证得结论;
(2)连接FM,证得四边形AMFD是菱形,得出AN=NF,求得M是AB的中点,利用勾股定理求得AN,进一步得出NE,进一步利用勾股定理求得DE的长即可.
(1)证明:∵平行四边形ABCD
∴AD=BC,AD//BC
∴∠DAF=∠CEF,∠ADF=∠ECF
∵点F为CD中点
∴DF=CF
∴△ADF≌△ECF(AAS)
∴AD=CE
∴BC=CE.
(2)如图,连接FM,

∵DM平分∠ADF,AF平分∠DAB,AB∥DC,AD∥BC,
∴∠DAF=∠BAF=DFN,∠ADM=∠FDM=∠AMD,
∴AD=DF=AM,
∴四边形AMFD是菱形,
∴AF⊥DM,DN=MN=![]() DM=1,
DM=1,
又∵DF=FC,DC=AB=6,
∴AM=3,
∴AN=![]() ,
,
∴AF=2AN=4![]() ,
,
∵AF=EF,
∴NE=AE-AN=6![]() ,
,
∴DE=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】数轴上A,B,C三点对应的数a,b,c满足(a+40)2+|b+10|=0,B为线段AC的中点.

(1)直接写出A,B,C对应的数a,b,c的值.
(2)如图1,点D表示的数为10,点P,Q分别从A,D同时出发匀速相向运动,点P的速度为6个单位/秒,点Q的速度为1个单位/秒.当点P运动到C后迅速以原速返回到A又折返向C点运动;点Q运动至B点后停止运动,同时P点也停止运动.求在此运动过程中P,Q两点相遇点在数轴上对应的数.
(3)如图2,M,N为A,C之间两点(点M在N左边,且它们不与A,C重合),E,F分别为AN,CM的中点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的2016年6月份的日历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( )

A. 27 B. 51 C. 69 D. 72
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.
(1)求正比例函数的解析式;
(2)在x轴上能否找到一点P,使△AOP的面积为5?若存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有若干根长度相同的火柴棒,用a根火柴棒,按如图①摆放时可摆成m个正方形,用b根火柴棒,按如图②摆放时可摆成2n个正方形.(m、n是正整数)

(1)如图①,当m=4时,a=______;如图②,当b=52时,n=______;
(2)当若干根长度相同的火柴棒,既可以摆成图①的形状,也可以摆成图②的形状时,m与n之间有何数量关系,请你写出来并说明理由;
(3)现有61根火柴棒,用若干根火柴棒摆成图①的形状后,剩下的火柴棒刚好可以摆成图②的形状.请你直接写出一种摆放方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年5月,我国南方某省A、B两市遭受严重洪涝灾害,1.5万人被迫转移,邻近县市C、D获知A、B两市分别急需救灾物资200吨和300吨的消息后,决定调运物资支援灾区.已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市.已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用别为每吨15元和30元,设从D市运往B市的救灾物资为x吨.
(1)请填写下表
A(吨) | B(吨) | 合计(吨) | |
C |
|
| 240 |
D |
| x | 260 |
总计(吨) | 200 | 300 | 500 |
(2)设C、D两市的总运费为w元,求w与x之间的函数关系式,并写出自变量x的取值范围;
(3)经过抢修,从D市到B市的路况得到了改善,缩短了运输时间,运费每吨减少m元(m>0),其余路线运费不变.若C、D两市的总运费的最小值不小于10320元,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
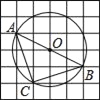
【题目】如图,在6×6的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点,作△ABC的外接圆⊙O,则弧AC的长等于( )
A. π B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象l与坐标轴分别交于点E,F,与双曲线y=﹣![]() (x<0)交于点P(﹣1,n),且F是PE的中点,直线x=a与l交于点A,与双曲线交于点B(不同于A),PA=PB,则a=________.
(x<0)交于点P(﹣1,n),且F是PE的中点,直线x=a与l交于点A,与双曲线交于点B(不同于A),PA=PB,则a=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
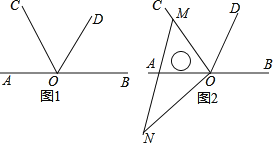
【题目】如图1,点O为直线AB上一点,过点O作射线OC,OD,使射线OC平分∠AOD.
(1)当∠BOD=50°时,∠COD= °;
(2)将一直角三角板的直角顶点放在点O处,当三角板MON的一边OM与射线OC重合时,如图2.
①在(1)的条件下,∠AON= °;
②若∠BOD=70°,求∠AON的度数;
③若∠BOD=α,请直接写出∠AON的度数(用含α的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com