
����Ŀ����ƽ��ֱ������ϵxOy�У���A������Ϊ(0��m)����m��0����B������Ϊ(n��0)�����߶�AB�Ƶ�B��ת90�����ֱ�õ��߶�B P1��B P2���Ƶ�P1��P2Ϊ��A���ڵ�B�������������ͼ1Ϊ��A���ڵ�B�������������ʾ��ͼ��
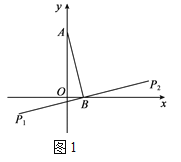
(1)��֪��A(0��4)��
�ٵ���B������ֱ�Ϊ(1��0)��(-2��0)ʱ����A���ڵ�B�����������������ֱ�Ϊ ��
�ڵ㣨x��y���ǵ�A���ڵ�B�������������ֱ��д��y��x֮��Ĺ�ϵʽ��
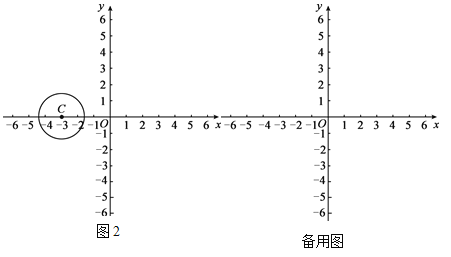
(2)��ͼ2����C������Ϊ(-3��0)����CΪԲ�ģ� ![]() Ϊ�뾶��Բ�����ڡ�C�ϴ��ڵ�A���ڵ�B�������������ֱ��д����A��������m��ȡֵ��Χ��
Ϊ�뾶��Բ�����ڡ�C�ϴ��ڵ�A���ڵ�B�������������ֱ��д����A��������m��ȡֵ��Χ��
���𰸡���1���٣�-3��-1������5��1������-6��2������2��-2������y=x-4��y=-x-4.
��2��-5��m��-1��1��m��5
�����������������(1)����![]() ��x���ڵ�M����
��x���ڵ�M����![]() ��x���ڵ�N��������֪������֤
��x���ڵ�N��������֪������֤![]() ��
��![]() ��
��![]() ������ȫ�������ε����ʿɵ�
������ȫ�������ε����ʿɵ�![]() =OB=
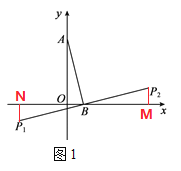
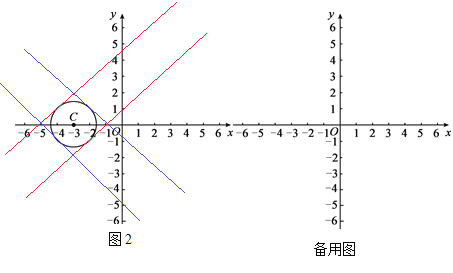
=OB= ![]() ��OA=BM=BN������A(0��4)������B������Ϊ(1��0)ʱ��������õ�A���ڵ�B�ġ�����㡱������ֱ�Ϊ��-3��-1������5��1��������A(0��4)������B������Ϊ(-2��0)ʱ��������õ�A���ڵ�B�ġ�����㡱������ֱ�Ϊ��-6��2������2��-2�������ɢٿ�֪��x=y+4��-x-y=4�����ɵ�y��x֮��Ĺ�ϵʽΪy=x-4��y=-x-4����2�����A������Ϊ��0��m�����㣨x��y���ǵ�A���ڵ�B�ġ�����㡱���ɣ�1���ķ����ɵ�y=x-m��y=-x-m����ֱ��y=x-m����ʱ����ͼ��ͼ�еĺ��ߣ�������ֱ��y=x-m��x�ᡢy����Χ�ɵ�������Ϊ����ֱ�������Ρ����ߵ����ʡ����ɶ��������m=1����m=5�����ɵ�1��m��5����ֱ��y=-x-m����ʱ����ͼ��ͼ�е����ߣ���ͬ���ɵ�-5��m��-1�����Ե�A��������m��ȡֵ��ΧΪ-5��m��-1��1��m��5.
��OA=BM=BN������A(0��4)������B������Ϊ(1��0)ʱ��������õ�A���ڵ�B�ġ�����㡱������ֱ�Ϊ��-3��-1������5��1��������A(0��4)������B������Ϊ(-2��0)ʱ��������õ�A���ڵ�B�ġ�����㡱������ֱ�Ϊ��-6��2������2��-2�������ɢٿ�֪��x=y+4��-x-y=4�����ɵ�y��x֮��Ĺ�ϵʽΪy=x-4��y=-x-4����2�����A������Ϊ��0��m�����㣨x��y���ǵ�A���ڵ�B�ġ�����㡱���ɣ�1���ķ����ɵ�y=x-m��y=-x-m����ֱ��y=x-m����ʱ����ͼ��ͼ�еĺ��ߣ�������ֱ��y=x-m��x�ᡢy����Χ�ɵ�������Ϊ����ֱ�������Ρ����ߵ����ʡ����ɶ��������m=1����m=5�����ɵ�1��m��5����ֱ��y=-x-m����ʱ����ͼ��ͼ�е����ߣ���ͬ���ɵ�-5��m��-1�����Ե�A��������m��ȡֵ��ΧΪ-5��m��-1��1��m��5.
���������
��1���٣�-3��-1������5��1������-6��2������2��-2��.
��y=x-4��y=-x-4.
��2��-5��m��-1��1��m��5



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
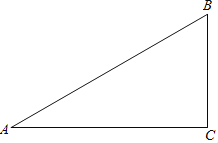
����Ŀ����֪����ͼ������ABC�У���A��30�㣬��B��60�㡣
��1������B��ƽ����BD����AC�ڵ�D����AB���е�E��Ҫ�߹���ͼ��������ͼ�ۼ�������д��
����֤������
��2������DE����֤����ADE����BDE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʽ8x��5y���Ա�ʾ�ܶ����壬���磺��x��ʾƻ��ÿǧ�˵�Ǯ����y��ʾ�㽶ÿǧ�˵�Ǯ������8x��5y��ʾ��8 kgƻ����5 kg�㽶������Ǯ���������8x��5y������һ��ʵ�����壮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
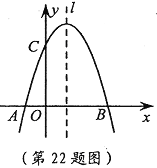
����Ŀ��������10�֣���ͼ����֪������![]() ��
��![]() �ύ��A��B���㣬��
�ύ��A��B���㣬��![]() �ύ�ڵ�C����B������Ϊ��3��0����
�ύ�ڵ�C����B������Ϊ��3��0����
��1����m��ֵ�������ߵĶ������ꣻ
��2����P�������߶Գ���![]() �ϵ�һ�����㣬��PA+PC��ֵ��Сʱ�����P�����ꡣ
�ϵ�һ�����㣬��PA+PC��ֵ��Сʱ�����P�����ꡣ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A������Ϊ��3��4������A����x��ԳƵĵ�������ǣ� ��
A.����3��4��
B.��3����4��
C.����3����4��
D.��4��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������Ǻ���ֵ���ü����������A �� B�Ķ��� ��
��1��sinA=0.7��sinB=0.01��
��2��cosA=0.15��cosB=0.8��
��3��tanA=2.4��tanB=0.5 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�����������ڣ��������������ȵ�С������ֽƬ��������ֽƬ��ס���������24ƽ�����ף���δ��ס�������С������������ķ�֮һ����3ƽ�����ף���������ε�����ǣ���λ��ƽ�����ף���������.
A.40
B.25
C.26
D.36
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com