练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知多项式ax2＋bx＋c＝(2x－1)(x＋3)，求a＋b＋c的值．

    【答案】4.

    【解析】

    先把(2x－1)(x＋3)展开，再根据原式相等即可得到a，b，c的值，最后即可得到答案.

    因为(2x－1)(x＋3)＝2x2＋6x－x－3＝2x2＋5x－3，

    所以a＝2，b＝5，c＝－3，所以a＋b＋c＝4.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB＝90°，BC的垂直平分线EF交BC于点D ， 交AB于点E ， 且BE＝BF ， 添加一个条件，仍不能证明四边形BECF为正方形的是（　　）.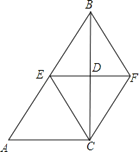

    A.BC＝AC
    B.CF⊥BF
    C.BD＝DF
    D.AC＝BF

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中xOy中，抛物线的顶点在x轴上．

    （1）求抛物线的表达式；

    （2）点Q是x轴上一点，

    ①若在抛物线上存在点P，使得∠POQ=45°，求点P的坐标；

    ②抛物线与直线y=2交于点E，F（点E在点F的左侧），将此抛物线在点E，F（包含点E和点F）之间的部分沿x轴平移n个单位后得到的图象记为G，若在图象G上存在点P，使得∠POQ=45°，求n的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于任意自然数，试说明代数式n（n+7）-（n-3）（n-2）的值都能被6整除．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】看图填空：已知如图，AD⊥BC于D，EG⊥BC与G，∠E=∠1，求证：AD平分∠BAC．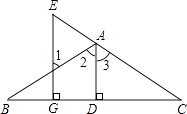
    证明：∵AD⊥BC于D，EG⊥BC于G（）
    ∴∠ADC=90°，∠EGC=90°（）
    ∴∠ADC=∠EGC
    ∴AD∥EG（）
    ∴∠1=∠2（）
    ∠E=∠3（）
    又∵∠E=∠1（）
    ∴∠2=∠3
    ∴AD平分∠BAC（）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某书店老板去图书批发市场购买某种图书．第一次用1200元购书若干本，并按该书定价7元出售，很快售完．由于该书畅销，第二次购书时，每本书的批发价已比第一次提高了20%，他用1500元所购该书数量比第一次多10本．当按定价售出200本时，出现滞销，便以定价的4折售完剩余的书．试问该老板这两次售书总体上是赔钱了，还是赚钱了（不考虑其它因素）？若赔钱，赔多少？若赚钱，赚多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，点A的坐标为(0，m)，且m≠0，点B的坐标为(n，0)，将线段AB绕点B旋转90°，分别得到线段B P1，B P2，称点P1，P2为点A关于点B的“伴随点”，图1为点A关于点B的“伴随点”的示意图．

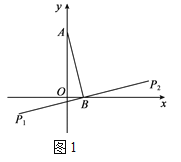
    (1)已知点A(0，4)，

    ①当点B的坐标分别为(1，0)，(-2，0)时，点A关于点B的“伴随点”的坐标分别为 ；

    ②点（x，y）是点A关于点B的“伴随点”，直接写出y与x之间的关系式；

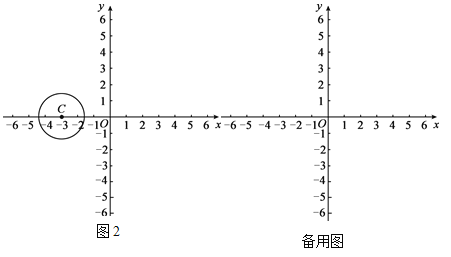
    (2)如图2，点C的坐标为(-3，0)，以C为圆心， 为半径作圆，若在⊙C上存在点A关于点B的“伴随点”，直接写出点A的纵坐标m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明每天从家去学校上学行走的路程为900米，某天他从家去上学时以每分30米的速度行走了450米，为了不迟到他加快了速度，以每分45米的速度行走完剩下的路程，设该天小明上学行走t分时行走的路程为S米，则当l5＜t≤25时，s与t之间的函数关系是（　　）
    A.s=30t
    B.s=900-30t
    C.S=45t-225
    D.s=45t-675

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若二次函数y=(1-k)x2-2x-1的图象与x轴有2个交点，则k的取值范围是_________.

    查看答案和解析>>

    同步练习册答案