
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D , 交AB于点E , 且BE=BF , 添加一个条件,仍不能证明四边形BECF为正方形的是( ).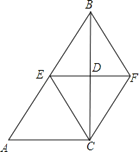
A.BC=AC
B.CF⊥BF
C.BD=DF
D.AC=BF
【答案】D
【解析】∵EF垂直平分BC , ∴BE=EC , BF=CF , ∵BF=BE , ∴BE=EC=CF=BF , ∴四边形BECF是菱形;当BC=AC时,∵∠ACB=90°,则∠A=45,∴∠EBC=45°,∴∠EBF=2∠EBC=2×45°=90°,∴菱形BECF是正方形,故选项A不符合题意;当CF⊥BF时,利用正方形的判定得出,菱形BECF是正方形,故选项B不符合题意;当BD=DF时,利用正方形的判定得出,菱形BECF是正方形,故选项C不符合题意;当AC=BF时,无法得出菱形BECF是正方形,故选项D符合题意.
【考点精析】关于本题考查的线段垂直平分线的性质和正方形的判定方法,需要了解垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角才能得出正确答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列调查中,适宜采用普查方式的是( )
A. 了解一批灯泡的使用寿命B. 了解外地游客对天柱山的印象
C. 了解本班同学早餐是否有喝牛奶的习惯D. 了解我国初中学生的视力情况
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.

(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
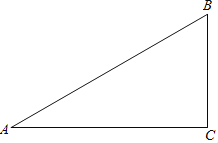
【题目】已知:如图,在△ABC中,∠A=30°,∠B=60°。
(1)作∠B的平分线BD,交AC于点D;作AB的中点E(要求:尺规作图,保留作图痕迹,不必写作
法和证明);
(2)连接DE,求证:△ADE≌△BDE。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强调查“每人每天的用水量”这一问题时,收集到80个数据,最大数据是70升,最小数据是42升,若取组距为4,则应分为_________组绘制频数分布表.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com