
【题目】在平面直角坐标系中xOy中,抛物线![]() 的顶点在x轴上.
的顶点在x轴上.
(1)求抛物线的表达式;
(2)点Q是x轴上一点,
①若在抛物线上存在点P,使得∠POQ=45°,求点P的坐标;
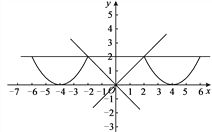
②抛物线与直线y=2交于点E,F(点E在点F的左侧),将此抛物线在点E,F(包含点E和点F)之间的部分沿x轴平移n个单位后得到的图象记为G,若在图象G上存在点P,使得∠POQ=45°,求n的取值范围.
【答案】(1)抛物线的表达式为![]() ;
;
(2)①点P的坐标为![]() 或
或 ![]() ②n的取值范围是
②n的取值范围是![]()
【解析】试题分析:(1)把函数解析式化为顶点式, ![]() , 因顶点在x轴上,可得m-2=0,即m=2,即可求得函数的解析式
, 因顶点在x轴上,可得m-2=0,即m=2,即可求得函数的解析式![]() ;(2)由∠POQ=45°可知点P是直线y=x与抛物线的交点,令
;(2)由∠POQ=45°可知点P是直线y=x与抛物线的交点,令![]() ,解得x的值即可得点P的坐标;(3)当E点移动到点(2,2)时,n=2,当F点移动到点(-2,2)时,n=-6,由图象可知,符合题意的n的取值范围是
,解得x的值即可得点P的坐标;(3)当E点移动到点(2,2)时,n=2,当F点移动到点(-2,2)时,n=-6,由图象可知,符合题意的n的取值范围是![]() .
.
试题解析:
(1)![]() .
.
由题意,可得m-2=0.
∴![]() .
.
∴![]() .
.
(2)①由题意得,点P是直线![]() 与抛物线的交点.
与抛物线的交点.
∴![]() .
.
解得 ![]() ,
, ![]() .
.
∴P点坐标为![]() 或
或 ![]() .
.
②当E点移动到点(2,2)时,n=2.
当F点移动到点(-2,2)时,n=-6.
由图象可知,符合题意的n的取值范围是![]() .
.


科目:初中数学 来源: 题型:
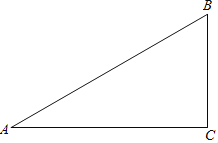
【题目】已知:如图,在△ABC中,∠A=30°,∠B=60°。
(1)作∠B的平分线BD,交AC于点D;作AB的中点E(要求:尺规作图,保留作图痕迹,不必写作
法和证明);
(2)连接DE,求证:△ADE≌△BDE。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强调查“每人每天的用水量”这一问题时,收集到80个数据,最大数据是70升,最小数据是42升,若取组距为4,则应分为_________组绘制频数分布表.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】代数式8x+5y可以表示很多意义,例如:若x表示苹果每千克的钱数,y表示香蕉每千克的钱数,则8x+5y表示买8 kg苹果和5 kg香蕉共花的钱数.请你给8x+5y赋予另一种实际意义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列锐角三角函数值,用计算器求锐角A , B的度数 .
(1)sinA=0.7,sinB=0.01;
(2)cosA=0.15,cosB=0.8;
(3)tanA=2.4,tanB=0.5 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com