
【题目】看图填空:已知如图,AD⊥BC于D,EG⊥BC与G,∠E=∠1,求证:AD平分∠BAC. 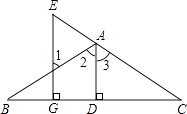
证明:∵AD⊥BC于D,EG⊥BC于G()
∴∠ADC=90°,∠EGC=90°()
∴∠ADC=∠EGC
∴AD∥EG()
∴∠1=∠2()
∠E=∠3()
又∵∠E=∠1()
∴∠2=∠3
∴AD平分∠BAC().
【答案】已知;垂直的定义;同位角相等,两直线平行;两直线平行,内错角相等;两直线平行,同位角相等;已知;角平分线的定义
【解析】证明:∵AD⊥BC于D,EG⊥BC于G(已知) ∴∠ADC=90°,∠EGC=90°(垂直的定义)
∴∠ADC=∠EGC
∴AD∥EG(同位角相等,两直线平行)
∴∠1=∠2(两直线平行,内错角相等)
∠E=∠3(两直线平行,同位角相等)
又∵∠E=∠1(已知)
∴∠2=∠3
∴AD平分∠BAC(角平分线的定义).
所以答案是:已知;垂直的定义;同位角相等,两直线平行;两直线平行,内错角相等;两直线平行,同位角相等;已知;角平分线的定义.
【考点精析】关于本题考查的平行线的判定与性质,需要了解由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能得出正确答案.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.

(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF;
(3)在(2)的条件下,若DE=4,DF=3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】代数式8x+5y可以表示很多意义,例如:若x表示苹果每千克的钱数,y表示香蕉每千克的钱数,则8x+5y表示买8 kg苹果和5 kg香蕉共花的钱数.请你给8x+5y赋予另一种实际意义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算错误的是( )
A. (6a+1)(6a﹣1)=36a2﹣1 B. (a3﹣8)(﹣a3+8)=a9﹣64
C. (﹣m﹣n)(m﹣n)=n2﹣m2 D. (﹣a2+1)(﹣a2﹣1)=a4﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
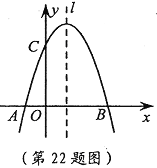
【题目】(本题10分)如图,已知抛物线![]() 与
与![]() 轴交于A,B两点,与
轴交于A,B两点,与![]() 轴交于点C,点B的坐标为(3,0)。
轴交于点C,点B的坐标为(3,0)。
(1)求m的值及抛物线的顶点坐标;
(2)点P是抛物线对称轴![]() 上的一个动点,当PA+PC的值最小时,求点P的坐标。
上的一个动点,当PA+PC的值最小时,求点P的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com