
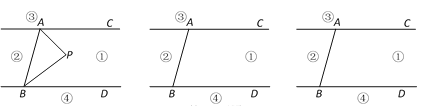
����Ŀ����ͼ��ֱ��AC��BD������AB��ֱ��AC��BD���߶�AB��ƽ��ֳɢ١��ڡ��ۡ����ĸ����֣��涨�����ϸ��㲻�����κβ��֣�������P����ij������ʱ������PA��PB�����ɡ�PAC����APB����PBD�����ǣ�(��ʾ���й����˵�������غϵ���������ɵĽ���0��)
(1)������P���ڵڢٲ���ʱ���С�APB����PAC����PBD����˵�����ɣ�
(2)������P���ڵڢڲ���ʱ����APB����PAC����PBD�Ƿ������������������д����PAC����APB����PBD�����ǵĵ�����ϵ(����˵������)��
(3)������P�ڵڢ۲���ʱ��̽����PAC����APB����PBD֮��Ĺ�ϵ��д���㷢�ֵ�һ������������˵����

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧС�����λͬѧ������������ѧ¥֮��ľ��룬��ͼ��������ѧ¥AB��CD֮����һ���۳أ�AB��BD��CD��BD����һͬѧ��A���ó�����Ȫ��E��ĸ���Ϊ42�㣬��һͬѧ��C����E��ĸ���Ϊ45�㣨��B��E��D��ͬһֱ���ϣ�������ͬѧ�Ѿ���ѧУ�����Ҳ��¥��AB=15m��CD=20m����������ѧ¥֮��ľ���BD��
�������ȷ��0.1m���ο����ݣ�sin42���0.67��cos42���0.74��tan42���0.90��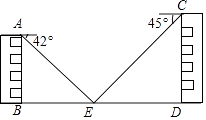
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����е�ʽ����1��13��![]() ��12��22����2��13+23��
��12��22����2��13+23��![]() ��22��32����3��13+23+33��
��22��32����3��13+23+33��![]() ��32��42����4��13+23+33+43��
��32��42����4��13+23+33+43��![]() ��42��52��
��42��52��![]()
����������ʽ�Ĺ��ɣ�����������⣺
��1��д����5����ʽ��_____��
��2��д����n����ʽ���ú���n�Ĵ���ʽ��ʾ����
��3����s����������s��2��Ӧ���㷢�ֵĹ��ɣ�����![]() ��s2����s+1��2��
��s2����s+1��2��![]() ����s��1��2��s2��
����s��1��2��s2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
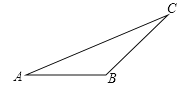
����Ŀ����ͼ����գ�
������ͼ����ABC�ĸ�AD(��ע����D��λ��)��
����������ABC������AD����ƽ��2cm��õ�����A1B1C1��
��������ͼ��ƽ���������ʣ���BB1=_____cm��AC��A1C1��λ�ù�ϵ��_____��������ϵ�ǣ�________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ǵ�����ƽ��·ͼ����ͼ�У�������Ϊ�����������ᣬ�������ĸ����ۣ�
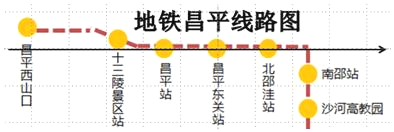
�ٵ���ʾ��ƽ����վ�ĵ��Ӧ����Ϊ0����ʾ��ƽվ�ĵ��Ӧ����Ϊ��1.5ʱ����ʾ������վ�ĵ��Ӧ����Ϊ1.2��
�ڵ���ʾ��ƽ����վ�ĵ��Ӧ����Ϊ0����ʾ��ƽվ�ĵ��Ӧ����Ϊ��15ʱ����ʾ������վ�ĵ��Ӧ����Ϊ12��
�۵���ʾ��ƽ����վ�ĵ��Ӧ����Ϊ1����ʾ��ƽվ�ĵ��Ӧ����Ϊ��14ʱ����ʾ������վ�ĵ��Ӧ����Ϊ13��
�ܵ���ʾ��ƽ����վ�ĵ��Ӧ����Ϊ2����ʾ��ƽվ�ĵ��Ӧ����Ϊ��28ʱ����ʾ������վ�ĵ��Ӧ����Ϊ26��
���������У�������ȷ���۵�����ǣ�������
A. �٢ڢ�B. �ڢۢ�C. �٢�D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ȫ������̣�
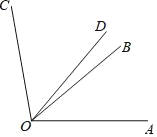
��֪����ͼ����AOB��40������BOC��60����ODƽ�֡�AOC�����BOD�Ķ�����
�⣺�ߡ�AOC����AOB+���� ����
�֡ߡ�AOB��40������BOC��60����
���AOC���� ������
��ODƽ�֡�AOC��
���AOD���� ����AOC���� ������
���AOD��50����
���BOD����AOD������ ����
���BOD���� ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��˳���ݹ�˾�ɼס���������A�ؽ�һ����Ʒ��������B�أ��׳���0.5h���ҿ�ʼ����������ȼ���1��h������B�أ���ͼ���߶�OP��MN�ֱ��ʾ�ס���������A�صľ���S��km����ʱ��t��h���Ĺ�ϵ��a��ʾA��B����֮��ľ��룮����ͼ�е���Ϣ����������⣺ 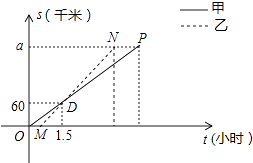
��1���ֱ����ס����������ٶȼ�a��ֵ��
��2���ҳ�����B�غ���ԭ���������أ����ʼ׳�����B�غ��Զ����ٶ��������ٷ��أ��������ҳ�ͬʱ�ص�A�أ�����ͼ�л����ס��������ڷ��ع�������A�صľ���S��km����ʱ��t��h���ĺ���ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ͼ��
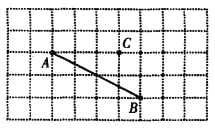
��1������C��AB��ƽ����CD��
��2������C��AB������������ΪE��
��3���߶�CE�ij����ǵ�C��ֱ��_______�ľ��룻
��4������CA��CB�����߶�CA��CB��CE�У��߶�_______��̣����ɣ�_______��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com